题目内容
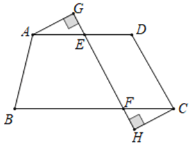
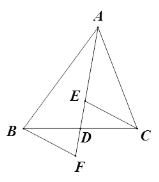
【题目】如图, AD是![]() 的中线,E,F分别是AD和AD延长线上的点,且
的中线,E,F分别是AD和AD延长线上的点,且![]() ,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有________(填上正确的序号)
,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有________(填上正确的序号)
【答案】①②③④.
【解析】
根据三角形中线的定义可得BD=CD,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE,最后根据等底等高的三角形的面积相等判断出②正确.
∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
 ,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BF∥CE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的是①②③④.
故答案为:①②③④.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目