题目内容
【题目】在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CFF=45°
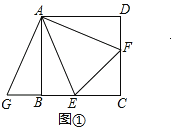
(1) 将△ADF绕点A顺时针旋转90 °,得到△ABG(如图1),求证:BE+DF=EF;
(2) 若直线EF与AB、AD的延长线分别交于点M、N(如图2),求证:![]()
(3) 将正方形改为长与宽不相等的矩形,其余条件不变(如图3),直接写出线段EF、BE、DF之间的数量关系.

【答案】(1)见解析;(2)见解析;(3) ![]() =2
=2![]() .
.
【解析】
(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=![]() DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,结合勾股定理以及相等线段可得(GH+BE)2+(BE-GH)2=EF2,所以2(DF2+BE2)=EF2.
(1)证明:∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
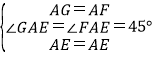 ,
,
∴△AGE≌△AFE(SAS);
(2)证明:设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.

则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=![]() DF,
DF,
∴a-BE=a-DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=![]() BM=
BM=![]() DF=NF,
DF=NF,
∴EF2=ME2+NF2;
(3)解:EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.

由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM-GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE-GH)2=EF2,
即2(DF2+BE2)=EF2

【题目】对某批乒乓球质量进行随机调查,结果如下表;
随机抽取的乒乓球数 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
优等品数 | 7 | 16 | 43 | 81 | 164 | 410 | 820 |
优等频率 | 0.7 | 0.8 | 0.86 | 0.81 | 0.82 | 0.82 |
(1)填表格中的空为_______.
(2)根据上表估计,在这批乒乓球中任取一个球,它为优等品的概率大约是________.(保留两位小数点)
(3)学校需要500个乒乓球的优等品,那么可以推测出最有可能进这批货的乒乓球个数是多少合适?(结果保留整数)






