题目内容
【题目】已知:如图,D是△ABC边BC上一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AC=2AE.

【答案】见解析.
【解析】
延长AE到F,使EF=AE,连接DF,,可证明△ABE≌△FDE,则∠BAE=∠EFD
,再由外角的性质得出∠ADF=∠ADC,则△ADF≌△ADC,则AF=AC,从而得出AC=2AE.
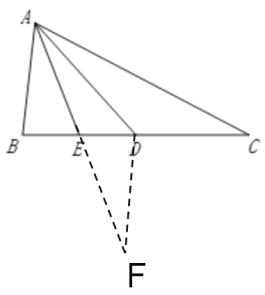
证明:延长AE到F,使EF=AE,连接DF
∵AE是△ABD的中线.
∴BE=ED
在△ABE和△FDE中,
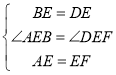
∴△ABE≌△FDE(SAS)
∴AB=DF,∠BAE=∠EFD
∵∠ADB是△ADC的外角
∴∠DAC+∠ACD=∠ADB=∠BAD
∴∠BAE+∠EAD=∠BAD
∠BAE=∠EFD
∴∠EFD+∠EAD=∠DAC+∠ACD
∴∠ADF=∠ADC
∵AB=DC
∴DF=DC
在△ADF和△ADC中,
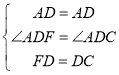
∴△ADF≌△ADC(SAS)
∴AF=AC
∵AF=AE+EF,AE=ED
∴AC=2AE

练习册系列答案
相关题目
【题目】某公园门票的收费标准如下:
门票类别 | 成人票 | 儿童票 | 团体票(限5张及以上) |
价格(元/人) | 100 | 40 | 60 |
有两个家庭分别去该公园游玩,每个家庭都有5名成员,且他们都选择了最省钱的方案购买门票,结果一家比另一家少花40元,则花费较少的一家花了( )元.
A.300B.260C.240D.220