题目内容
【题目】已知:如图,在正方形ABCD,E是BC边上一点,F是CD的中点,且AE = DC + CE. 求证:AF平分∠DAE.

【答案】见解析
【解析】
延长BC、AF交于G,由AAS证明△FCG≌△FDA,得出CG=DA,由已知条件得出AE=GE,由等腰三角形的性质得到∠EAF=∠G,即可得出结论.
延长BC、AF交于G,如图:
∵四边形ABCD是正方形,∴AD∥BC,DA=DC,∠FCB=∠D=90°,
∴∠DAF=∠G,∠FCG=90°,∴∠FCG=∠D.
在△FCG和△FDA中,∵ 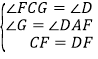 ,
,
∴△FCG≌△FDA(AAS),
∴CG=DA.
∵AE=DC+CE,∴AE=CG+CE=GE,∴∠EAF=∠G,∴∠DAF=∠EAF,∴AF平分∠DAE.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目