��Ŀ����
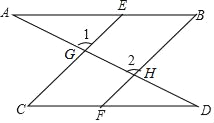
����Ŀ����ͼ��������ABCD�У���ABC=��BAC=90�㣬��AD��ȡһ��E������ABE��ֱ��BE�۵���ʹ��A����BD�ϵ�G����EG���ӳ��߽�ֱ��BC�ڵ�F��
��1����̽��AE��ED��DG֮���к�������ϵ��˵�����ɣ�
��2���жϡ�ABG���BFE�Ƿ����ƣ����Խ��۸���֤����
��3����AD=a��AB=b��BC=c��
�ٵ��ı���EFCDΪƽ���ı���ʱ����a��b��cӦ����Ĺ�ϵ��
���ڢٵ������£���b=2ʱ��a��ֵ��Ψһ�ģ����C�Ķ�����
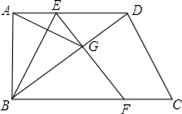
���𰸡���1��AE2+DG2=ED2�����ɼ���������2����ABG�ס�BFE�����ɼ���������3����a2+b2=ac���ڡ�C=45�㣮
�������������������1�����۵��õ���EGB=��EAB=90�㣬�����ù��ɶ������ɣ�
��2�����жϡ�EAB�ա�EGB��Ȼ���ABG=��EFB�͡�BAG=��FBE�����õȵ����ۣ�
��3���ɣ�2���еĽ��ۡ�ABG�ס�BFE�ó����ۣ����ж�����ABD�ס�HCD�ó�����ʽ�����ҵ����ۣ����ɸ���ϵ���Ĺ�ϵ���жϼ��㼴�ɣ�
�����������1��AE2+DG2=ED2��
���ɣ����۵����ʵã���EAB�ա�EGB��AE=GE����EGB=��EAB=90�㣬
����Rt��EGD�У��ɹ��ɶ����ã�EG2+DG2=ED2��
��AE2+DG2=ED2��
��2����ABG�ס�BFE��
���ɣ��ߡ�ABC=��BAC=90�㣬��AD��BC�����AEB=��EBF��
�ߡ�EAB�ա�EGB����AEB=��BEG�����EBF=��BEF����FE=FB������FEBΪ���������Σ�
�ߡ�ABG+��GBF=90�㣬��GBF+��EFB=90�㣬���ABG=��EFB��
�ڵ�����ABG�͡�FEB�У���BAG=��180��-��ABG����2����FBE=��180��-��EFB����2��
���BAG=��FBE��
���ABG�ס�BFE��
��3���١ߡ�ABG�ס�BFE�����EFB=��GBA�����C=��ABG��
�ߡ�DAB=��DHC=90�㣬���ABD�ס�HCD����![]() ��
��
��![]() ����a2+b2=ac��
����a2+b2=ac��
�ڵ�b=2ʱ�������a��һԪ���η���a2��ac+22=0������Ϊa1��a2��
�ã�a1a2=c��0��a1+a2=4��0����a1��0��a2��0��
������a1=a2�����=0����c2��16=0��
��c��0����c=4����a=2����HΪBC�е㣬��ABHDΪ�����Σ���DH=HC��
���C=45�㣮