Question

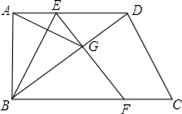
【题目】如图，在△ABC中，AB=BC，点E在边AB上，EF⊥AC于F．

（1）尺规作图：过点A作AD⊥BC于点D（保留作图痕迹，不写作法）；（2）求证：∠CAD=∠AEF；（3）若∠ABC=45°，AD与EF交于点G，求证：EG=2AF．

Answer 1

【答案】（1）图形见解析；（2）证明过程见解析；（3）证明过程见解析

【解析】

试题分析：（1）、根据高线的作法作出图形；（2）、根据AB=BC得出∠C=∠BAC，根据垂直得出∠CDA=∠EFA=90°，根据三角形内角和定理得出∠DAC=∠AEF；（3）、过点E作EM∥BC，题意得出EGN≌△ANM，从而说明EG=AM，根据等腰三角形的三线合一定理得出AM=2AF，则EG=2AF.

试题解析：（1）、作图略

（2）、∵BC=BA ∴∠C=∠BAC ∵AD⊥BC，EF⊥AC ∴∠CDA=∠EFA=900

∴1800－∠C －∠CDA=1800－∠BAC －∠EFA 即∠DAC=∠AEF

（3）、过点E作EM∥BC分别交AD、AC于点N、M

∵EM∥BC ∴∠MEA=∠B=450，∠ENA=∠ADB=900， ∴△AEN为等腰直角三角形，∠ANM=900，

∴NE=NA ∴∠ENA=∠ANM ∵EF⊥AC， ∴∠EFA=900 ∴∠ENA=∠EFA

又∵∠EGN=∠AGF ∴1800－∠ENA －∠EGN=1800－∠EFA －∠AGF 即∠NEG=∠NAM

∴△ENG≌△ANM ∴EG=AM ∵BC=BA ∴∠C=∠BAC

∵EM∥BC ∴∠EMA=∠C ∴∠EMA=∠BAC ∴△EMA为等腰三角形

又 ∵EF⊥MA ∴AM=2AF ∴EG=2AF