Question

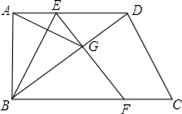
【题目】在正方形ABCD中，E为CD上一点，F为BC延长线上一点，且CE＝CF.

（1）求证：△BCE≌△DCF；

（2）若∠FDC＝30°，求∠BEF的度数．

Answer 1

【答案】见解析

【解析】试题分析：

(1) 结合条件观察图形可知，在待求证的这组全等三角形中，有一组对应角∠BCE与∠DCF互补，根据四边形ABCD是正方形的条件易知∠BCE=∠DCF. 以这组对应角为着眼点进一步观察图形易知，作为正方形ABCD边的BC与DC相等，条件中又已知CE=CF，故可以利用SAS证明这组三角形全等.

(2) 求∠BEF的度数就是求∠BEC+∠CEF的度数. 在Rt△DCF中易知∠DFC的度数. 利用第(1)小题的结论可知∠BEC=∠DFC，从而得到∠BEC的度数. 利用条件可以得出△ECF为等腰直角三角形的结论，从而得到∠CEF的度数. 综合上面的结果即得∠BEF的度数.

试题解析：

(1) 证明：∵四边形ABCD是正方形，

∴BC=DC，∠BCD=90°，

∴∠DCF=∠BCD=90°，即∠BCE=∠DCF=90°，

∵在△BCE与△DCF中：

，

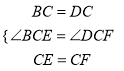∴△BCE≌△DCF (SAS).

(2) ∠BEF的度数为105°. 求解过程如下.

∵∠FDC=30°，∠DCF=90°，

∴在Rt△DCF中，∠DFC=90°-∠FDC=90°-30°=60°，

∵△BCE≌△DCF，

∴∠BEC=∠DFC=60°，

∵CE=CF，∠DCF=90°，

∴△ECF为等腰直角三角形，

∴∠CEF=∠CFE=45°，

∵∠BEC=60°，∠CEF=45°，

∴∠BEF=∠BEC+∠CEF=60°+45°=105°.