题目内容
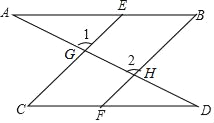
【题目】如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
【答案】(1)CE∥BF,AB∥CD.理由见解析.(2)证明见解析.
【解析】试题分析:(1)根据同位角相等,两直线平行可得CE∥FB,进而可得∠C=∠BFD,再由条件∠B=∠C可得∠B=∠BFD,从而可根据内错角相等,两直线平行得AB∥CD;
(2)根据(1)可得AB∥CD,再根据两直线平行,内错角相等可得∠A=∠D.
试题解析:(1)CE∥BF,AB∥CD.理由:
∵∠1=∠2,
∴CE∥FB,
∴∠C=∠BFD,
∵∠B=∠C,
∴∠B=∠BFD,
∴AB∥CD;
(2)由(1)可得AB∥CD,
∴∠A=∠D.

练习册系列答案
相关题目