题目内容
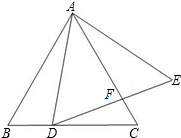
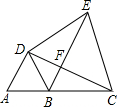
已知如图，B是AC上一点，△ABD和△DCE都是等边三角形．
（1）求证：AC=BE；
（2）若BE⊥DC，求∠BDC的度数．
（1）求证：AC=BE；
（2）若BE⊥DC，求∠BDC的度数．
（1）证明：∵△ABD和△DCE都是等边三角形，
∴∠ADB=∠CDE=60°，AD=BD，CD=DE．
∴∠ADB+∠BDC=∠BDC+∠FDE，即∠ADC=∠BDE．
∴△ADC≌△BDE．
∴AC=BE．
（2）∵△DCE是等边三角形，
∴DE=CE，又∵BE⊥DC，
∴F为DC的中点（三线合一），
∴BE是CD的中垂线．
∴DB=CB．又△ABD是等边三角形，
∴AB=DB=BC，
∴△ADC是直角三角形（三角形一边上的中线等于这边的一半，则这边所对的角为直角），
∵∠A=60，
∴∠BDC=∠ACD=90°-∠A=90°-60°=30°．
∴∠ADB=∠CDE=60°，AD=BD，CD=DE．
∴∠ADB+∠BDC=∠BDC+∠FDE，即∠ADC=∠BDE．
∴△ADC≌△BDE．
∴AC=BE．
（2）∵△DCE是等边三角形，
∴DE=CE，又∵BE⊥DC，
∴F为DC的中点（三线合一），
∴BE是CD的中垂线．
∴DB=CB．又△ABD是等边三角形，
∴AB=DB=BC，
∴△ADC是直角三角形（三角形一边上的中线等于这边的一半，则这边所对的角为直角），
∵∠A=60，
∴∠BDC=∠ACD=90°-∠A=90°-60°=30°．
练习册系列答案
相关题目
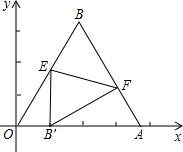正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．
