题目内容
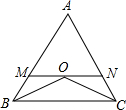
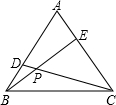
如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<
,则P1C长的取值范围是( )

| 3 |
| 2 |
A.1<P1C<
| B.
| C.
| D.
|

∵反射角等于入射角,∴∠P0P1C=∠P2P1A=∠P2P3B,
又∵∠C=∠A=∠B=60°,
∴△P0P1C∽△P2P1A∽△P2P3B,
∴
=
=
.
设P1C=x,P2A=y,则P1A=2-x,P2B=2-y.
∴
=
=
,
∴
,
∴x=
(2+P3B).
又∵1<BP3<
,
∴1<x<
.
即P1C长的取值范围是:1<P1C<
.
故选A.
又∵∠C=∠A=∠B=60°,
∴△P0P1C∽△P2P1A∽△P2P3B,
∴
| P0C |
| P1C |
| P2A |
| P1A |
| P2B |
| P3B |
设P1C=x,P2A=y,则P1A=2-x,P2B=2-y.
∴
| 1 |
| x |
| y |
| 2-x |
| 2-y |
| P3B |
∴
|
∴x=
| 1 |
| 3 |
又∵1<BP3<
| 3 |
| 2 |
∴1<x<
| 7 |
| 6 |
即P1C长的取值范围是:1<P1C<
| 7 |
| 6 |
故选A.

练习册系列答案
相关题目