题目内容
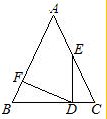
△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,BN与AM相交于Q点,∠AQN等于多少度?
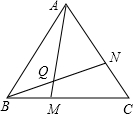

证法一.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
,
△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC-∠MAB=60°-∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°-∠ANB-∠MAN,
∠AQN=180°-(∠ANB+∠MAN),
=180°-120°=60°,
∠BOM=∠AQN=60°(全等三角形对应角相等).
证法二.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
∴△AMB≌△BNC(SAS)
∵∠ANB=∠C+∠NBC=60°+∠NBC
∠MAN=∠BAC-∠MAB
又∵∠NBC=∠MAB(全等三角形对应角相等)
∴∠ANB+∠MAN=120°
又∵∠ANQ+∠MAN+∠AQN=180°
∴∠AQN=180°-∠ANB-∠MAB
∠AQN=180°-(∠ANB+∠MAN)
=180°-120°=60°
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中

|
△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC-∠MAB=60°-∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°-∠ANB-∠MAN,
∠AQN=180°-(∠ANB+∠MAN),
=180°-120°=60°,
∠BOM=∠AQN=60°(全等三角形对应角相等).
证法二.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
|
∴△AMB≌△BNC(SAS)
∵∠ANB=∠C+∠NBC=60°+∠NBC
∠MAN=∠BAC-∠MAB
又∵∠NBC=∠MAB(全等三角形对应角相等)
∴∠ANB+∠MAN=120°
又∵∠ANQ+∠MAN+∠AQN=180°
∴∠AQN=180°-∠ANB-∠MAB
∠AQN=180°-(∠ANB+∠MAN)
=180°-120°=60°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目