Question

【题目】（12分）某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本（万元/吨）与产量（吨）之间是一次函数关系，函数与自变量的部分对应值如下表：

（吨）	10	20	30
（万元/吨）	45	40	35

（1）求与的函数关系式，并写出自变量的取值范围；

（2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）

（3）市场调查发现，这种产品每月销售量（吨）与销售单价（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）

Answer 1

【答案】（1）=，；（2）40吨；（3）375万元．

【解析】

试题（1）利用待定系数法解得y与x的函数关系式，根据产量至少为10吨，但不超过55吨写出自变量x的取值范围；

（2）根据总成本=每吨成本×总产量边上总成本，当总成本为1200时，解得x的值；

（3）应用待定系数法求得每月销售量（吨）与销售单价（万元/吨）之间的函数关系式，可知当=25时，，根据这个月的利润等于销量×每吨的利润．

试题解析：解：（1）设=，

则，∴，

∴=，

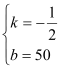自变量的取值范围为：；

（2）由（1）知=1200，即=1200，

，

解得 ，（舍去），

∴该产品的总产量为40吨；

（3）设=，

则，∴，

∴=，

当=25时，，

利润=25×（45-）=25×15=375，

答：第一个月的利润为375万元．