题目内容
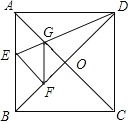
【题目】在四边形ABCD中，AB=CD，E，F分别为边BC与AD的中点，AE∥CD，延长BA，CD，分别与EF的延长线交于点G，H，连接AH，ED.
（1）求证：AH∥ED；
（2）求证：AE=AG.
【答案】（1）（2）见解析.
【解析】
（1）证△AEF≌△DHF. 得AE=DH.由AE∥DH，得四边形AEDH是平行四边形.（2）连接AC，设AC的中点为O，连接OE，OF.根据三角形中位线性质得OF∥CD，OF=
CD，OE∥AB，OE=AB，OE=OF. 得∠OFE=∠OEF，∠DHE =∠AGE. 由AE∥DH，得∠DHE =∠AEG. 所以∠AGE =∠AEG.
（1）∵AE∥CD，
∴∠AEF=∠DHF，∠FAE=∠FDH.
∵AF=FD，
∴△AEF≌△DHF.
∴AE=DH.
∵AE∥DH，
∴四边形AEDH是平行四边形.
∴AH∥ED.
（2）连接AC，设AC的中点为O，连接OE，OF.
∵E，F分别为边BC与AD的中点，
∴OF∥CD，OF=CD，OE∥AB，OE=AB.
∴∠OFE=∠DHE，∠OEF=∠AGE.
∵AB=CD，
∴OE=OF.
∴∠OFE=∠OEF.
∴∠DHE =∠AGE.
∵AE∥DH，
∴∠DHE =∠AEG.
∴∠AGE =∠AEG.
∴AE=AG.
【题目】（12分）某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本
（万元/吨）与产量
（吨）之间是一次函数关系，函数
与自变量的部分对应值如下表：
| 10 | 20 | 30 |
| 45 | 40 | 35 |
（1）求
与
的函数关系式，并写出自变量的取值范围；
（2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）
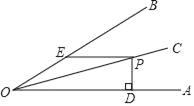
（3）市场调查发现，这种产品每月销售量
（吨）与销售单价
（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）
