��Ŀ����
����Ŀ����������������ʯ������Ȼ�ֺ�Ƶ����������ɼ���������ͲƲ���ʧ��Ϊ�˸��õ����á�������֡�������������ز��Ŷ�ij��ѧѧ����������֡���֪���ʲ�ȡ��������ķ��������ʾ����飬��������Ϊ���dz��˽⡱�����Ƚ��˽⡱���������˽⡱�͡����˽⡱�ĸ��ȼ���С�����ݵ�������������ͼ1��2��ͳ��ͼ��������ṩ����Ϣ�ش����⣺
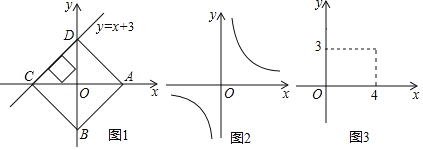
��1�����ε����У�����������________��
��2������ͳ��ͼ�С������˽⡱��������Ӧ������Բ�Ľ���________���ڸ�У2000��ѧ�����������һ��ѧ�����ԡ�������֡����˽�ĸ��ʵĹ���ֵΪ________��
��3������ͼ2�в�ȫƵ���ֲ�ֱ��ͼ��

ͼ1 ͼ2
���𰸡���1��400�� ��2��144�㣬![]() ����3���������.
����3���������.
��������
��1���������dz��˽�������������ռ�İٷֱ���ʽ���㼴����������ʾ������ѧ��������
��2������������˽�����ѧ����ռ�İٷֱȣ��ٳ���360�������㼴�ɵý⣻��������˽�����ѧ����ռ�İٷֱȼ��ɣ�
��3������ѧ�������������ԱȽ��˽��ѧ����ռ�İٷֱȣ�����Ƚ��˽����������ȫƵ���ֲ�ֱ��ͼ���ɣ�
��1����������ã�
80��20%��400���ˣ���
������������400��
�ʴ�Ϊ��400��
��2���������˽�����������Ӧ������Բ�Ľ��ǣ�![]() ��360�㣽144�㣬
��360�㣽144�㣬
����������������˽�ĸ��ʵĹ���ֵΪ��![]() ��
��![]() ��
��
�ʴ�Ϊ��144�㣬![]() ��
��
��3�����Ƚ��˽���������Ϊ��400��35%��140�ˣ���ȫ��ͼ��

 ����С����ͬ������ϵ�д�
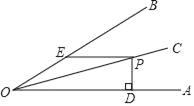
����С����ͬ������ϵ�д�����Ŀ����12����ij��������һ�ֲ�Ʒ������������Ϊ10�֣���������55��ʱ��ÿ�ֵijɱ�![]() ����Ԫ/���������
����Ԫ/���������![]() ������֮����һ�κ�����ϵ������
������֮����һ�κ�����ϵ������![]() ���Ա���
���Ա���![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
| 10 | 20 | 30 |
| 45 | 40 | 35 |
��1����![]() ��
��![]() �ĺ�����ϵʽ����д���Ա���
�ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����Ͷ���������ֲ�Ʒ���ܳɱ�Ϊ1200��Ԫʱ����ò�Ʒ���ܲ�������ע���ܳɱ�=ÿ�ֳɱ����ܲ�����
��3���г����鷢�֣����ֲ�Ʒÿ��������![]() �����������۵���
�����������۵���![]() ����Ԫ/����֮��������ͼ��ʾ�ĺ�����ϵ���ó���һ���°�ͬһ���۵����������ֲ�Ʒ25�֣�������ó���һ�����������ֲ�Ʒ��õ���������ע������=�ۼ����ɱ���
����Ԫ/����֮��������ͼ��ʾ�ĺ�����ϵ���ó���һ���°�ͬһ���۵����������ֲ�Ʒ25�֣�������ó���һ�����������ֲ�Ʒ��õ���������ע������=�ۼ����ɱ���