题目内容
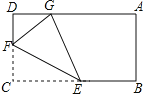
【题目】如图，在长方形ABCD中，点E，F分别是BC，DC上的动点．沿EF 折叠△CEF，使点C的对称点G落在AD上，若AB=3，BC=5，求CF的取值范围．
【答案】
≤CF≤3
【解析】
当点E与B重合时，CF最小，先利用勾股定理求出AG，设CF=FG=
，在Rt△ABG中，利用勾股定理列出方程即可解决问题，当F与D重合时，CF最大，由此即可解决问题．
∵四边形ABCD是长方形，∴∠C=90°，BC=AD=5，CD=AB=3，
当点D与F重合时，CF最大=3，如图1所示：
当B与E重合时，CF最小，如图2所示：
在Rt△ABG中，∵BG=BC=5，AB=3，
∴AG=
=4，
∴DG=AD﹣AG=1，
设CF=FG=，
在Rt△DFG中，∵DF2+DG2=FG2，
∴
，∴x=
．
∴CF的取值范围为≤CF≤3
练习册系列答案
相关题目
【题目】（12分）某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本
（万元/吨）与产量
（吨）之间是一次函数关系，函数
与自变量的部分对应值如下表：
| 10 | 20 | 30 |
| 45 | 40 | 35 |
（1）求
与
的函数关系式，并写出自变量的取值范围；
（2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）
（3）市场调查发现，这种产品每月销售量
（吨）与销售单价
（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）
