题目内容
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP 的长为![]() ,四边形CDPE的面积为
,四边形CDPE的面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据含有30°角的直角三角形的性质和勾股定理求出![]() 的长,从而求出BP的长,然后求出BE的长;
的长,从而求出BP的长,然后求出BE的长;
(2)设AP= ![]() ,则BP=4—
,则BP=4—![]() ,根据含有30°角的直角三角形的性质和勾股定理求出PD和PE的长,再根据PD=PE列出方程即可.
,根据含有30°角的直角三角形的性质和勾股定理求出PD和PE的长,再根据PD=PE列出方程即可.
(3)分别用AP表示PD、PE、BE,再根据![]() 即可求出.
即可求出.
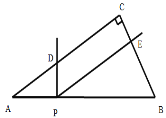
(1)在△ABC中,∠ACB=90°,∠A=30°,AB=4,
![]()
∵点D为AC边的中点
![]() ,
,
∵∠DPE=60°,过点P作AB的垂线交AC边与点D,
∴∠EPB=30°,∴EB ![]()
(2)设AP= ![]() ,则BP=4—
,则BP=4—![]() ,在两个含有30°的
,在两个含有30°的![]() 中得出:
中得出:
AD=2DP,BP=2BE,由勾股定理解得:![]() ,
,
∵PD=PE,∴![]() 解得
解得![]() 即有AP=
即有AP= ![]()
(3)由(2)知:AP= ![]() ,
,![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】(12分)某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本![]() (万元/吨)与产量
(万元/吨)与产量![]() (吨)之间是一次函数关系,函数
(吨)之间是一次函数关系,函数![]() 与自变量
与自变量![]() 的部分对应值如下表:
的部分对应值如下表:
| 10 | 20 | 30 |
| 45 | 40 | 35 |
(1)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
(3)市场调查发现,这种产品每月销售量![]() (吨)与销售单价
(吨)与销售单价![]() (万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
(万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)