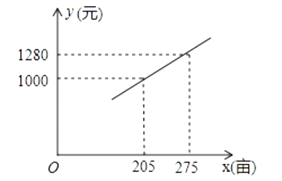
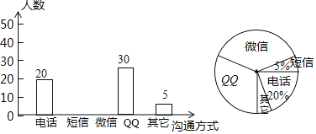
题目内容
【题目】如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为 _ ．
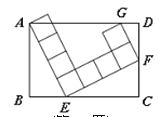
【答案】8
【解析】
根据AAS可以证明△ABE≌△ECF，得AB=CE，BE=CF；根据两角对应相等，可以证明△ECF∽△FDG，则DF：CE=FG：EF=1：2．设BE=x，则AB=2x，根据勾股定理求得x的值，进而求得矩形的面积．
根据等角的余角相等，得
∠BAE=∠CEF=∠DFG．
又∠B=∠C=∠D=90°，AE=EF=4，FG=2，
∴△ABE≌△ECF，△ECF∽△FDG．
∴AB=CE，BE=CF，DF：CE=FG：EF=1：2．
设BE=x，则AB=2x，根据勾股定理，得
x2+4x2=16，
x=
．
则矩形ABCD的面积为：2x×3x=6x2=
．
练习册系列答案
新思维寒假作业系列答案
相关题目
