Question

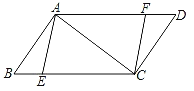
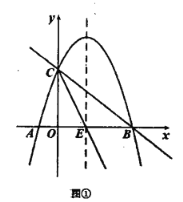
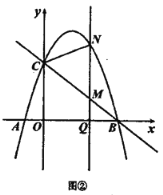
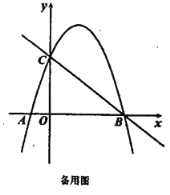
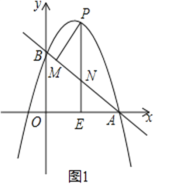
【题目】如图1，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．

（1）求抛物线的解析式和直线AB的函数表达式；

（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值．

Answer 1

【答案】（1） ， （2）m=2

【解析】

（1）令y＝0，求出抛物线与x轴交点，列出方程即可求出a，即可得出抛物线解析式，根据待定系数法可以确定直线AB解析式；

（2）由△PNM∽△ANE，推出，列出方程即可解决问题．

解：（1）令y＝0，则ax2＋（a＋3）x＋3＝0，

∴（x＋1）（ax＋3）＝0，

∴x＝1或，

∵抛物线y＝ax2＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），

∴＝4，

∴a＝，

∴抛物线解析式为：；

∵A（4，0），B（0，3），

设直线AB解析式为y＝kx＋b，则，

解得，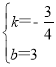

∴直线AB解析式为；

（2）如图1中，

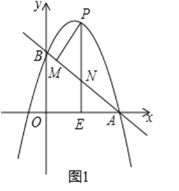
∵PM⊥AB，PE⊥OA，

∴∠PMN＝∠AEN，

∵∠PNM＝∠ANE，

∴△PNM∽△ANE，

∴，

∵NE∥OB，

∴，

∴AN＝（4m），

∵抛物线解析式为，

∴PN＝m2＋m＋3（m＋3）＝m2＋3m，

∴，

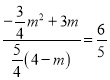解得m＝2．