题目内容
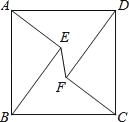
【题目】如图,在![]() 中,
中,![]() 为直径,
为直径,![]() 为弦.过
为弦.过![]() 延长线上一点
延长线上一点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】![]() 与
与![]() 相切;理由见解析;(2)
相切;理由见解析;(2)![]() ;
;
【解析】
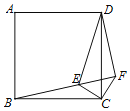
(1)连接OC,如图,利用圆周角定理得到∠ACB=90°,再根据斜边上的中线性质得MC=MG=ME,所以∠G=∠1,接着证明∠1+∠2=90°,从而得到∠OCM=90°,然后根据直线与圆的位置关系的判断方法可判断CM为⊙O的切线;
(2)先证明∠G=∠A,再证明∠EMC=∠4,则可判定△EFC∽△ECM,利用相似比先计算出CE,再计算出EF,然后计算ME﹣EF即可.
(1)CM与⊙O相切.理由如下:
连接OC,如图,∵GD⊥AO于点D,∴∠G+∠GBD=90°.
∵AB为直径,∴∠ACB=90°.
∵M点为GE的中点,∴MC=MG=ME,∴∠G=∠1.
∵OB=OC,∴∠B=∠2,∴∠1+∠2=90°,∴∠OCM=90°,∴OC⊥CM,∴CM为⊙O的切线;
(2)∵∠1+∠3+∠4=90°,∠5+∠3+∠4=90°,∴∠1=∠5,而∠1=∠G,∠5=∠A,∴∠G=∠A.
∵∠4=2∠A,∴∠4=2∠G,而∠EMC=∠G+∠1=2∠G,∴∠EMC=∠4,而∠FEC=∠CEM,∴△EFC∽△ECM,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,∴CE=4,EF=
,∴CE=4,EF=![]() ,∴MF=ME﹣EF=6﹣
,∴MF=ME﹣EF=6﹣![]() =
=![]() .
.

练习册系列答案
相关题目