题目内容
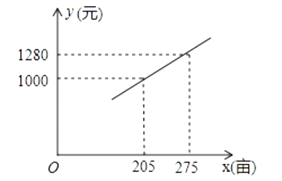
【题目】国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元.种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示.
(1)今年老王种粮可获得补贴_____________元;
(2)求y与x之间的函数关系式;
(3)若老王明年每亩的售粮收入能达到2100元,设老王明年种粮利润为w(元).(种粮利润=售粮收入-种粮成本+种粮补贴)
①求老王明年种粮利润w(元)与种粮面积x(亩)之间的函数关系式;
②当种粮面积为多少亩时,老王明年种粮利润最高?
【答案】(1)18000;(2)![]() ;(3)①
;(3)①![]() ,②当种粮255亩时,利润最高.
,②当种粮255亩时,利润最高.
【解析】
(1)根据每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,得出老王种粮可获得补贴数目;
(2)利用待定系数法求出一次函数解析式即可;
(3)根据明年每亩的售粮收入能达到2100元,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系为y=4x+180,进而得出W与x的函数关系式,再求二次函数的最值即可解决问题.
(1)∵国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,
∴今年老王种粮可获得补贴120×150=18000元;
故答案为:18000;
(2)假设函数解析式为y=kx+b,根据图象可以得出:图象过(205,1000),(275,1280),
将两点代入解析式得出:
![]() ,
,
解得:
![]() ,
,
则y与x之间的函数关系式为:y=4x+180;
(3)①根据题意得出:
W=(2100-y)x+120x
=[2100-(4x+180)]x+120x
=-4x2+2040x,
②x=-![]()
∵x≥150+50,x≤150+150,
∴200≤x≤300,
∴当x=255,W最大=260100(元).
当种粮面积为255亩时,总收入最高为260100元.

 阅读快车系列答案
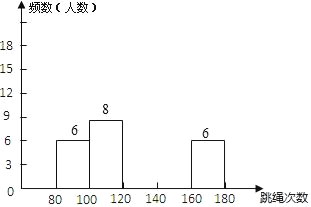
阅读快车系列答案【题目】为了解八年级500名学生的身体素质情况,体育老师从中随机抽取50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出如下频数分布表和频数分布直方图(不完整):
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
完成下列问题:
(1)请把上面的频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第 组;次数在140≤x<160这组的频率为 ;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120合格,试问该年级合格的学生有多少人?