题目内容
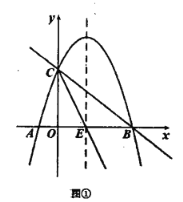
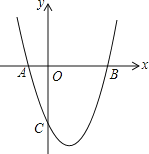
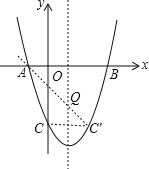
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点.
(1)求该抛物线的解析式;
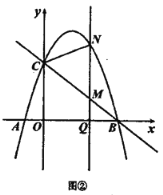
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=10,并求出此时P点的坐标;
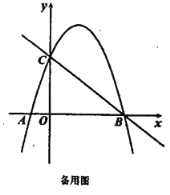
(3)设(1)中的抛物线交y轴交于C点,在该抛物线的对称轴上是否存在点Q,使△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
【答案】(1)y=x2-2x-3;(2)P点的坐标为(-2,5)或(4,5);(3)点Q的坐标为(1,-2).
【解析】
(1)根据抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点得到关于b和c的二元一次方程组,解方程组求出b和c的值即可;
(2)设动点P的坐标为(m,m2-2m-3),根据面积公式求出m的值即可;
(3)设点C关于对称轴的对称点为C′,连接AC′,直线AC′与对称轴的交点即为满足题意的Q点.
(1)∵抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2-2x-3;
(2)设动点P的坐标为(m,m2-2m-3),
若足S△PAB=10,
则![]() AB×|m2-2m-3|=10,
AB×|m2-2m-3|=10,
即2|m2-2m-3|=10,
解得m=4或m=-2;
当m=4时,m2-2m-3=5,
当m=-2时,m2-2m-3=5,
综上P点的坐标为(-2,5)或(4,5);
(3)设点C关于对称轴的对称点为C′,连接AC′,直线AC′与对称轴的交点即为满足题意的Q点;
∵y=x2-2x-3=(x-1)2-4,
∴抛物线对称轴为x=1,C′坐标为(2,-3),
设直线AC′的解析式为y=kx+b,
根据题意可得![]() ,
,
解得![]() ,
,
所以直线AC′的解析式为y=-x-1,
当x=1时,y=-2,
即点Q的坐标为(1,-2).

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】为了解八年级500名学生的身体素质情况,体育老师从中随机抽取50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出如下频数分布表和频数分布直方图(不完整):
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
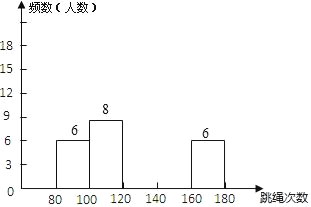
完成下列问题:
(1)请把上面的频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第 组;次数在140≤x<160这组的频率为 ;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120合格,试问该年级合格的学生有多少人?