题目内容
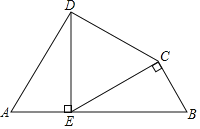
【题目】如图,四边形ABCD中,∠A=∠B=60°,∠ADC=90°,∠BCD=150°,点E是AB边上一点,DE⊥AB,EC⊥BC.

(1)试判断△DEC的形状,并说明理由.
(2)若BC=3,BE=6.求AB和AD的长.
【答案】(1)△DEC的形状为等边三角形,理由见解析;(2)AB=9,AD=6.
【解析】
(1)△DEC的形状为等边三角形,由已知条件易求∠EDC=∠ECD=60°,进而可证明△DEC的形状为等边三角形;
(2)易证△AED≌△ECB,由全等三角形的性质即可求出AB和AD的长.
(1)△DEC的形状为等边三角形,理由如下:
∵∠A=60°,∠ADC=90°,
∴∠ADE=30°,
∴∠DEC=60°,
∵EC⊥BC,
∴∠ECD=90°,
又∵∠BCD=150°,
∴∠DCE=60°,
∴∠EDC=∠ECD=60°,
∴△DEC的形状为等边三角形;
(2)∵△DEC的形状为等边三角形,
∴DE=CE,
在△AED和△ECB中
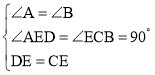 ,
,
∴△AED≌△ECB(AAS),
∴AD=BE=6,AE=BC=3,
∴AB=BE+AE=9.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目