题目内容
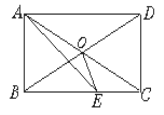
【题目】如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形 B. 若BD=CD,则四边形AEDF是菱形
C. 若AD垂直平分BC,则四边形AEDF是矩形 D. 若AD平分∠BAC,则四边形AEDF是菱形
【答案】D
【解析】
结合已知条件根据矩形的判定方法与菱形的判定方法逐一进行判断即可得.
A、AD⊥BC,不能判断出四边形AEDF是矩形,故A选项错误;
B、BD=CD与四边形AEDF是菱形没有任何关系,故B选项错误;
C、AD垂直平分BC与四边形AEDF是矩形没有任何关系,故C选项错误;
D、∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴∠BAD=∠ADF.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠CAD=∠ADF,
∴AF=DF,
∴平行四边形AEDF是菱形,
故选D.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
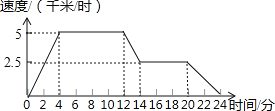
【题目】某天放学后,小敏徒步回家,如图所示,反映了她的速度与时间的变化关系.
(1)请你根据图象填写下表:
时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
速度/(千米/时) |
(2)根据图象或表格你能叙述一下小敏行走的情况吗?