题目内容
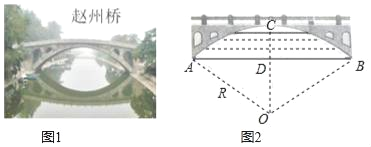
【题目】赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,
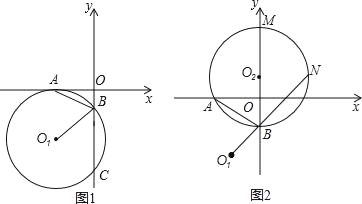
(1)如图1,尺规作图,找到桥弧所在圆的圆心O(保留作图痕迹);
(2)如图2,求桥弧AB所在圆的半径R.
【答案】(1)如图所示见解析;(2)桥弧AB所在圆的半径R为25米.
【解析】
(1)由垂径定理知,垂直于弦的直径是弦的中垂线,故作AB,BC的中垂线交于点O,则点O是桥弧所在圆的圆心;
(2)首先连接OA,由(1)可得:△AOD为直角三角形,D是AB的中点,CD=10,即可求得AD的长,然后在Rt△AOD中,由勾股定理得,OA2=AD2+OD2,即可求得拱桥的半径R.
(1)如图1所示;
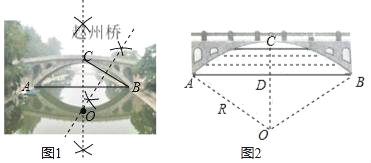
(2)连接OA.如图2.
由(1)中的作图可知:△AOD为直角三角形,D是AB的中点,CD=10,
∴AD=![]() AB=20.
AB=20.
∵CD=10,
∴OD=R﹣10.
在Rt△AOD中,由勾股定理得,OA2=AD2+OD2,
∴R2=202+(R﹣10)2.
解得:R=25.
即桥弧AB所在圆的半径R为25米.

练习册系列答案
相关题目