题目内容
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

【答案】(1)2-![]() ;(2)2-
;(2)2-![]() ;(3)3
;(3)3![]() -4.
-4.
【解析】
(1)求出![]() ,根据勾股定理求出
,根据勾股定理求出![]() ,即可求出
,即可求出![]() ;
;
(2)求出![]() ,根据全等三角形的性质得出
,根据全等三角形的性质得出![]() 即可;
即可;
(3)延长![]() 交
交![]() 于
于![]() ,证
,证![]() ,得出比例式,代入即可求出答案.
,得出比例式,代入即可求出答案.
解:(1)∵四边形ABCD是正方形,
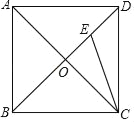
∴∠ABC=∠ADC=90°,
∠DBC=∠BCA=∠ACD=45°,
∵CE平分∠DCA,
∴∠ACE=∠DCE=![]() ∠ACD=22.5°,
∠ACD=22.5°,
∴∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°,
∵∠DBC=45°,
∴∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE,
∴BE=BC=![]() ,
,
在Rt△ACD中,由勾股定理得:BD=![]() =2,
=2,
∴DE=BD﹣BE=2﹣![]() ;
;
(2)∵FE⊥CE,
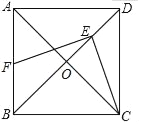
∴∠CEF=90°,
∴∠FEB=∠CEF﹣∠CEB=90°﹣67.5°=22.5°=∠DCE,
∵∠FBE=∠CDE=45°,BE=BC=CD,
∴△FEB≌△ECD,
∴BF=DE=2﹣![]() ;
;
(3)延长GE交AB于F,
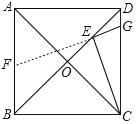
由(2)知:DE=BF=2﹣![]() ,
,
由(1)知:BE=BC=![]() ,
,
∵四边形ABCD是正方形,
∴AB∥DC,
∴△DGE∽△BFE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:DG=3![]() ﹣4.
﹣4.

练习册系列答案
相关题目