题目内容
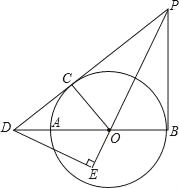
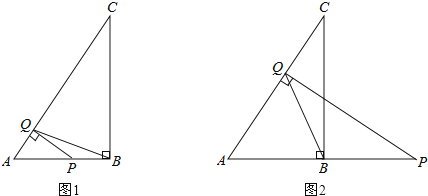
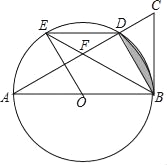
【题目】如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
根据直径所对的圆周角是直角即可进行判断BC是⊙O的切线;
连接OD, 利用扇形面积ODE-△OBD=阴影部分的面积,即可求出答案.
证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠A=∠DEB,∠DEB=∠DBC,
∴∠A=∠DBC,
∵∠DBC+∠ABD=90°,
∴BC是⊙O的切线;
(2)连接OD,
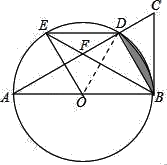
∵BF=BC=2,且∠ADB=90°,
∴∠CBD=∠FBD,
∵OE∥BD,
∴∠FBD=∠OEB,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠CBD=∠OEB=∠OBE=![]() ∠ADB=
∠ADB=![]() 90°=30°,
90°=30°,
∴∠C=60°,
∴AB=![]() BC=2
BC=2![]() ,
,
∴⊙O的半径为![]() ,
,
∴阴影部分的面积=扇形DOB的面积﹣三角形DOB的面积=![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目