题目内容
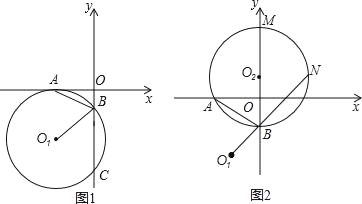
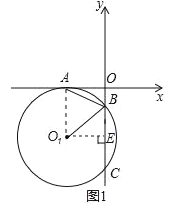
【题目】如图1在平面直角坐标系中,⊙O1与x轴切于A(﹣3,0)与y轴交于B、C两点,BC=8,连AB.
(1)求证:∠ABO1=∠ABO;
(2)求AB的长;
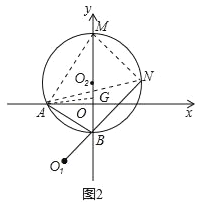
(3)如图2,过A、B两点作⊙O2与y轴的正半轴交于M,与O1B的延长线交于N,当⊙O2的大小变化时,得出下列两个结论:①BM﹣BN的值不变;②BM+BN的值不变.其中有且只有一个结论正确,请判断正确结论并证明.
【答案】(1)见解析;(2)![]() ;(3)①BM﹣BN的值不变,理由见解析.
;(3)①BM﹣BN的值不变,理由见解析.
【解析】
(1)连接O1A,由圆O1与x轴切于A,根据切线的性质得到O1A垂直于OA,由OB与AO垂直,根据平面内垂直于同一条直线的两直线平行,得到O1A与OB平行,根据两直线平行内错角相等,得到一对内错角相等,再由O1A=O1B,根据等边对等角可得出一对角相等,等量代换可得出∠ABO1=∠ABO,得证;
(2)作O1E⊥BC于点E,根据垂径定理得到E为BC的中点,由BC的长求出BE的长,再由A的横坐标得出OA的长,即为O1E的长,在直角三角形O1BE中,根据勾股定理求出O1B的长,用OE-BE求出OB的长,在直角三角形AOB中,根据勾股定理即可求出AB的长;
(3)两个结论中,①BM-BN的值不变正确,理由为:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,由∠ABO1为四边形ABMN的外角,根据圆内接四边形的外角等于它的内对角,可得出∠ABO1=∠NMA,再由∠ABO1=∠ABO,等量代换可得出∠ABO=∠NMA,然后利用同弧所对的圆周角相等可得出∠ABO=∠ANM,等量代换可得出∠NMA=∠ANM,根据等角对等边可得出AM=AN,再由同弧所对的圆周角相等,及OM=BN,利用SAS可得出三角形AMG与三角形ABN全等,根据全等三角形的对应边相等可得出AG=AB,由AO与BG垂直,根据三线合一得到O为BG的中点,根据OB的长求出BG的长,然后BM-BN=BM-MG=BG,由BG为常数得到BM-BN的长不变,得证.
(1)连接O1A,则O1A⊥OA,又OB⊥OA,
∴O1A∥OB,
∴∠O1AB=∠ABO,
又∵O1A=O1B,
∴∠O1AB=∠O1BA,
∴∠ABO1=∠ABO;
(2)作O1E⊥BC于点E,
∴E为BC的中点,
∵BC=8,
∴![]()
∵A(﹣3,0),
∴O1E=OA=3,
在直角三角形O1BE中,
根据勾股定理得:
![]()
∴O1A=EO=5,
∴BO=5﹣4=1,
在直角三角形AOB中,
根据勾股定理得: ![]()
(3)①BM﹣BN的值不变,理由为:
证明:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,
∵∠ABO1为四边形ABMN的外角,
∴∠ABO1=∠NMA,又∠ABO1=∠ABO,
∴∠ABO=∠NMA,又∠ABO=∠ANM,
∴∠AMN=∠ANM,
∴AM=AN,
∵∠AMG和∠ANB都为![]() 所对的圆周角,
所对的圆周角,
∴∠AMG=∠ANB,
在△AMG和△ANB中,
∵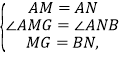
∴△AMG≌△ANB(SAS),
∴AG=AB,
∵AO⊥BG,
∴BG=2BO=2,
∴BM﹣BN=BM﹣MG=BG=2其值不变.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案