ЬтФПФкШн
ЁОЬтФПЁПЁОЮЪЬтЬсГіЁП
бЇЯАСЫШ§НЧаЮШЋЕШЕФХаЖЈЗНЗЈЃЈМДЁАSSSЁБЁЂЁАASAЁБЁЂЁАAASЁБЁЂЁАSSSЁБЃЉКЭжБНЧШ§НЧаЮШЋЕШЕФХаЖЈЗНЗЈЃЈМДЁАHLЁБЃЉКѓЃЌЮвУЧМЬајЖдЁАСНИіШ§НЧаЮТњзуСНБпКЭЦфжавЛБпЕФЖдНЧЖдгІЯрЕШЁБЕФЧщаЮНјаабаОПЃЎ
ЁОГѕВНЫМПМЁП
ЮвУЧВЛЗСНЋЮЪЬтгУЗћКХгябдБэЪОЮЊЃКдкЁїABCКЭЁїDEFжаЃЌAC=DFЃЌBC=EFЃЌЁЯB=ЁЯEЃЌШЛКѓЃЌЖдЁЯBНјааЗжРрЃЌПЩЗжЮЊЁАЁЯBЪЧжБНЧЁЂЖлНЧЁЂШёНЧЁБШ§жжЧщПіНјааЬНОПЃЎ
ЁОЩюШыЬНОПЁП
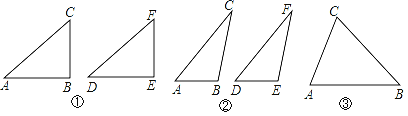
ЕквЛжжЧщПіЃКЕБЁЯBЪЧжБНЧЪБЃЌЁїABCЁеЁїDEFЃЎ
ШчЭМЂйЃЌдкЁїABCКЭЁїDEFЃЌAC=DFЃЌBC=EFЃЌЁЯB=ЁЯE=90ЁуЃЌИљОнЁЁ ЁЁЃЌПЩвджЊЕРRtЁїABCЁеRtЁїDEFЃЎ
ЕкЖўжжЧщПіЃКЕБЁЯBЪЧЖлНЧЪБЃЌЁїABCЁеЁїDEFЃЎ
ШчЭМЂкЃЌдкЁїABCКЭЁїDEFЃЌAC=DFЃЌBC=EFЃЌЁЯB=ЁЯEЃЌЧвЁЯBЃЌЁЯEЖМЪЧЖлНЧЃЌЧыФужЄУїЃКЁїABCЁеЁїDEFЃЈЬсЪОЃКЙ§ЕуCзїCGЁЭABНЛABЕФбгГЄЯпгкGЃЌЙ§ЕуFзїFHЁЭDEНЛDEЕФбгГЄЯпгкHЃЉЃЎ
ЕкШ§жжЧщПіЃКЕБЁЯBЪЧШёНЧЪБЃЌЁїABCКЭЁїDEFВЛвЛЖЈШЋЕШЃЎ
дкЁїABCКЭЁїDEFЃЌAC=DFЃЌBC=EFЃЌЁЯB=ЁЯEЃЌЧвЁЯBЃЌЁЯEЖМЪЧШёНЧЃЌЧыФуРћгУЭМЂлЃЌдкЭМЂлжагУГпЙцзїГіЁїDEFЃЌЪЙЁїDEFКЭЁїABCВЛШЋЕШЃЎ
ЁОД№АИЁПЃЈ1ЃЉHLЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉЁїDEFКЭЁїABCВЛШЋЕШЃЌЭММћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃК
ЃЈ1ЃЉгЩЬтвтПЩжЊЃЌДЫЪБЕУЕНЃКRtЁїABCЁеRtЁїDEFЕФвРОнЪЧЁАHLЁБЃЛ
ЃЈ2ЃЉШчЭМЃЌЗжБ№Й§ЕуCзїCGЁЭABНЛABЕФбгГЄЯпгкЕуGЃЌЙ§ЕуFзїFHЁЭDEНЛDEЕФбгГЄЯпгкHЃЌШЛКѓЯШгУЁАAASЁБжЄЁїCBGЁеЁїFEHЃЌНгзХгУЁАHLЁБжЄRtЁїACGЁеRtЁїDFHЃЌзюКѓгУЁАAASЁБжЄЁїABCЁеЁїDEFМДПЩЃЛ
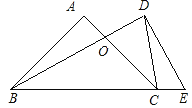
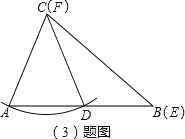
ЃЈ3ЃЉдкЭМ3жавдЕуCЮЊдВаФЃЌCAЮЊАыОЖзїЛЁНЛABгкЕуDЃЌЩшЕуEКЭЕуBжиКЯЃЌЕуFКЭЕуCжиКЯЃЌдђЭМжаЕФЁїABCКЭЁїDEFТњзуЬтФПжаЕФЬѕМўЃЌЕЋКмУїЯдЃЌДЫЪБСНИіШ§НЧаЮВЂВЛШЋЕШ.
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЁпдкЁїABCКЭЁїDEFжаЃКAC=DFЃЌBC=EFЃЌЁЯB=ЁЯE=90ЁуЃЌ
ЁрRtЁїABCЁеRtЁїDEFЃЈHLЃЉ.
МДДЫЪБХаЖЈСНШ§НЧаЮШЋЕШЕФвРОнЪЧЃКHLЃЛ
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуCзїCGЁЭABНЛABЕФбгГЄЯпгкGЃЌЙ§ЕуFзїFHЁЭDEНЛDEЕФбгГЄЯпгкHЃЌ
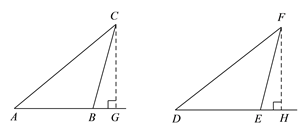
ЁпЁЯABC=ЁЯDEFЃЌЧвЁЯABCЁЂЁЯDEFЖМЪЧЖлНЧЃЌ
Ёр180ЁуЉЁЯABC=180ЁуЉЁЯDEFЃЌ
МДЁЯCBG=ЁЯFEHЃЌ
дкЁїCBGКЭЁїFEHжаЃЌ 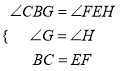 ЃЌ
ЃЌ
ЁрЁїCBGЁеЁїFEHЃЈAASЃЉЃЌ
ЁрCG=FHЃЌ
дкRtЁїACGКЭRtЁїDFHжаЃЌ ![]() ЃЌ
ЃЌ
ЁрRtЁїACGЁеRtЁїDFHЃЈHLЃЉЃЌ
ЁрЁЯA=ЁЯDЃЌ
дкЁїABCКЭЁїDEFжаЃЌ 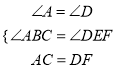 ЃЌ
ЃЌ
ЁрЁїABCЁеЁїDEFЃЈAASЃЉЃЛ
ЃЈ3ЃЉШчЭМЃЌЁїDEFКЭЁїABCжаЃЌAC=DFЃЌBC=EFЃЌЁЯB=ЁЯEЃЌТњзуСЫЬтФПжаЕФЬѕМўЃЌЕЋКмУїЯдЃЌЫќУЧВЛШЋЕШ.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ