题目内容
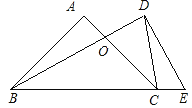
【题目】将一副直角三角板如图摆放，等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．
求证：△CDO是等腰三角形．
【答案】证明见解析.
【解析】试题分析：根据等腰三角形的性质和三角形的内角和定理求得∠BDC=∠BCD=75°，在根据三角形外角的性质求得∠DOC=75°，即可得∠DOC=∠BDC， 结论得证.
试题解析：
证明：∵在△BDC 中，BC=DB，
∴∠BDC=∠BCD．
∵∠DBE=30°
∴∠BDC=∠BCD=75°，
∵∠ACB=45°，
∴∠DOC=30°+45°=75°．
∴∠DOC=∠BDC，
∴△CDO是等腰三角形．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
