题目内容
【题目】已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.
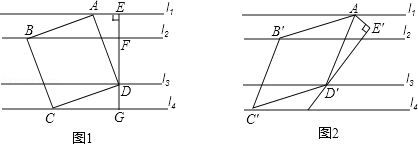
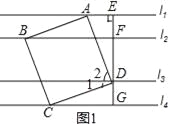
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.(可用备用图)
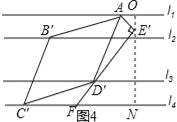
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.


【答案】(1)![]()
(2)![]() ,
, ![]()
(3)![]()
【解析】试题分析: (1)利用已知得出△AED≌△DGC(AAS),即可得出AE,以及正方形的边长;
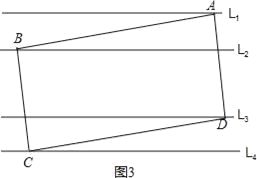
(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,则BE=1,BF=3,由四边形ABCD是矩形,∠ABC=90°,∠ABE+∠FBC=90°,根据∠ABE+∠EAB=90°,得到∠FBC=∠EAB,然后分类讨论,求得矩形的宽.
(3)首先过点E′作ON垂直于l1分别交l1,l2于点O,N,∠AEO=30°,则∠ED′N=60°,可求出AE=1,EO,EN,ED′的长,进而由勾股定理可知菱形的边长.
解:(1)∵l1∥l2∥l3∥l4,∠AED=90°
∴∠DGC=90°,
∵四边形ABCD为正方形
∴∠ADC=90°,AD=CD,∵∠ADE+∠2=90°,
∴∠1+∠2=90°,
∴∠1=∠ADE,
∵l3∥l4
∴∠1=∠DCG,
∠ADE=∠DCG,
在△AED与△DGC中,
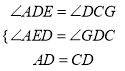 ,
,
∴△AED≌△GDC(AAS),
∴AE=GD=1,ED=GC=3,
∴AD=![]() ,
,
故答案为: ![]() ;
;
(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,
则BE=1,BF=3,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠FBC=90°,
∵∠ABE+∠EAB=90°,
∴∠FBC=∠EAB,
当AB<BC时,AB=![]() BC,
BC,
∴AE=![]() BF=
BF=![]() ,
,
∴AB=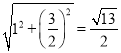 ;
;
如图3当AB>BC时,
同理可得:BC=![]() ,
,
∴矩形的宽为: ![]() ,
, ![]() ;
;
(3)如图4过点E′作ON垂直于l1分别交l1,l4于点O,N,
∵∠OAE′=30°,则∠E′FN=60°
∵AE′=AE=1,
故E′O=![]() ,E′N=
,E′N=![]() ,E′D′=
,E′D′=![]() ,
,
由勾股定理可知菱形的边长为: ![]() .
.