题目内容
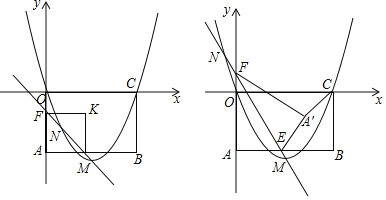
【题目】矩形OABC的边OC、OA分别位于x、y轴上，点A（0，﹣4）、B（6，﹣4）、C（6，0），抛物线y＝ax2+bx经过点O和点C，顶点M（3，﹣
），点N是抛物线上一动点，直线MN交直线AB于点E，交y轴于F，△A′EF是将△AEF沿直线MN翻折后的图形．
（1）求抛物线的解析式；
（2）当四边AEA′F是正方形时，求点N的坐标．
（3）连接CA′，求CA′的最小值．
【答案】（1）y＝
x2﹣3x；（2）
；（3）
.
【解析】
（1）根据待定系数法进行求解即可得到答案；
（2）根据正方形的性质，联立y＝﹣x﹣
与y＝x2﹣3x，即可得到答案；
（3）根据圆的性质即可得到答案.
解：（1）由已知可知C（6，0），M（3，﹣
），代入y＝ax2+bx，得
，
∴
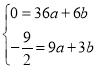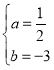
∴y＝x2﹣3x；
（2）当四边AEA′F是正方形时，
直线MF与x轴成角45°，
∴MF直线解析式为y＝﹣x﹣，
联立y＝﹣x﹣与y＝x2﹣3x，可得
x＝1或x＝3（舍）
∴N（1，﹣
）；
（3）A'的运动轨迹是以M为圆心MA为半径的圆，
∵MA＝3，MC＝
，
∴CA'最小值为；
练习册系列答案
相关题目
