题目内容
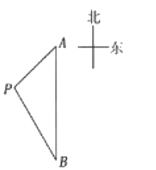
【题目】如图,一台起重机,他的机身高AC为21m,吊杆AB长为36m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m). (参考数据:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67,![]() ≈1.73)
≈1.73)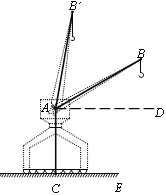
【答案】吊杆端点B离地面CE的最大高度为56.3cm,离机身AC的最大水平距离为31.1cm
【解析】
试题当∠BAD=30°时,吊杆端点B离机身AC的水平距离最大;
当∠B’AD=80°时,吊杆端点B’离地面CE的高度最大.
试题解析:当∠BAD=30°时,吊杆端点B离机身AC的水平距离最大;
当∠B’AD=80°时,吊杆端点B’离地面CE的高度最大.
作BF⊥AD于F,BG⊥CE于G,交AD于F’ .
在Rt△BAF中,cos∠BAF=![]() ,
,
∴AF=AB·cos∠BAF=40×cos30°≈34.6(cm).
在Rt△B’AF’中,sin∠BAF’=![]() ,
,
∴B’F’=AB’·sin∠B’AF’=40×sin80°≈39.2(cm).
∴B’G=B’F +F’G≈39.2+21=60.2(cm).
答:吊杆端点B离地面CE的最大高度约为60.2cm,离机身AC的最大水平距离约34.6cm.

【题目】(生活观察)甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价 | ||
质量 | 金额 | |
甲 |
|
|
乙 |
|
|
菜价 | ||
质量 | 金额 | |
甲 |
| ____元 |
乙 | ____千克 |
|
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价![]() 总金额总质量)
总金额总质量)
(数学思考)设甲每次买质量为![]() 千克的菜,乙每次买金额为
千克的菜,乙每次买金额为![]() 元的菜,两次的单价分别是
元的菜,两次的单价分别是![]() 元
元![]() 千克、
千克、![]() 元
元![]() 千克,用含有
千克,用含有![]() 、
、![]() 、
、![]() 、
、![]() 的式子,分别表示出甲、乙两次买菜的均价
的式子,分别表示出甲、乙两次买菜的均价![]() 、
、![]() .比较
.比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(知识迁移)某船在相距为![]() 的甲、乙两码头间往返航行一次,在没有水流时,船的速度为
的甲、乙两码头间往返航行一次,在没有水流时,船的速度为![]() 所需时间为:如果水流速度为
所需时间为:如果水流速度为![]() 时(
时(![]() ),船顺水航行速度为(
),船顺水航行速度为(![]() ),逆水航行速度为(
),逆水航行速度为(![]() ),所需时间为
),所需时间为![]() 请借鉴上面的研究经验,比较
请借鉴上面的研究经验,比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.