题目内容
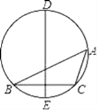
【题目】如图，在△ABC中，BC的垂直平分线交它的外接圆于D、E两点．若∠B=24°，∠C=106°，则
的度数为____
【答案】82°
【解析】
根据垂径定理的推理可判断DE为直径，根据垂径定理得到
，设△ABC的外接圆的圆心为O，连结OC、OA，如图，再利用三角形内角和计算出∠BAC=50°，利用圆周角定理得到∠EOC=∠BAC=50°，∠AOC=2∠B=48°，然后计算出∠AOD的度数，再根据
的度数等于它所对的圆心角的度数求解即可．
解：∵DE垂直平分BC，
∴DE为直径，，
设△ABC的外接圆的圆心为O，连结OC、OA，如图，
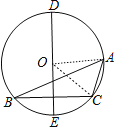
∵∠B=24°，∠C=106°，
∴∠BAC=180°-24°-106°=50°，
∴∠EOC=∠BAC=50°，
∵∠AOC=2∠B=48°，
∴∠AOD=180°-∠COE-∠AOC=180°-50°-48°=82°，
∴的度数为82°．
故答案为82°.
练习册系列答案
相关题目
