题目内容
【题目】在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,AB=CF.
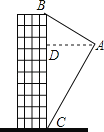
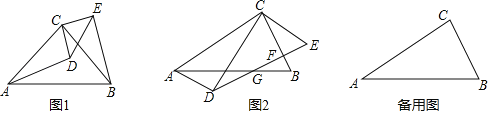
(1)如图1,求证:DF=DB;
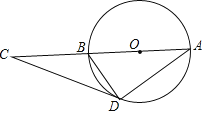
(2)如图2,若AF=![]() DF,在不添加任何辅助线和字母的情况下,请写出图中所有度数与3∠FAE的度数相等的角.
DF,在不添加任何辅助线和字母的情况下,请写出图中所有度数与3∠FAE的度数相等的角.

【答案】(1)证明见解析;(2)∠CAB,∠ABC,∠DFC,∠AFE与3∠FAE的度数相等,理由见解析.
【解析】
(1)由余角的性质可得∠DAB=∠DCE,由“AAS”可证△ADB≌△CDF,可得DF=BD;
(2)由等腰三角形的性质可求∠DFB=∠DBF=45°,即可求∠ABD=∠DBF+∠ABF=67.5°,由全等三角形的性质可得∠CAB=∠DCF=∠ABD=∠AFE=67.5°=3∠FAE.
(1)∵AD⊥BC,CE⊥AB
∴∠B+∠DAB=90°,∠B+∠DCE=90°
∴∠DAB=∠DCE,且∠ADB=∠ADC=90°,CF=AB
∴△ADB≌△CDF(AAS)
∴DF=BD
(2)∠CAB,∠ABC,∠DFC,∠AFE与3∠FAE的度数相等,
理由如下:如图:连接BF,

∵DF=DB,∠ADB=90°
∴∠DFB=∠DBF=45°,BF=![]() DF,且AF=
DF,且AF=![]() DF
DF
∴AF=BF
∴∠FAE=∠FBE
∴∠DFB=2∠FAE=2∠ABF=45°
∴∠FAE=∠FBE=22.5°
∴∠ABD=∠DBF+∠ABF=67.5°
∴∠ABD=3∠FAE
∵△ADB≌△CDF
∴∠DCF=∠ABD=∠AFE=67.5°=3∠FAE,
AD=CD
∴∠DAC=∠DCA=45°
∴∠CAB=67.5°=3∠FAE

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目