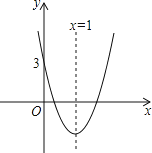题目内容
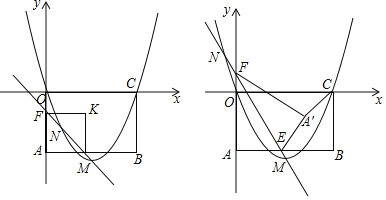
【题目】二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() 秒.
秒.
(1)求二次函数![]() 的表达式:
的表达式:
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积:
的面积:
(3)在直线![]() 上存在一点
上存在一点![]() ,当
,当![]() 是以
是以![]() 为直角的等腰直角三角形时,求此时点
为直角的等腰直角三角形时,求此时点![]() 的坐标;
的坐标;
(4)当![]() 时,在直线
时,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标
的坐标
【答案】(1)![]() (2)2(3)
(2)2(3)![]() (4)
(4)![]() 或
或![]()
【解析】
(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)根据题意得出AM,OM,设![]() 的解析式为:
的解析式为:![]() ,将点
,将点![]() 代入求出解析式,然后将
代入求出解析式,然后将![]() 分别代入
分别代入![]() 和
和![]() 中,得:
中,得:![]() ,再根据三角形面积公式,即可解答
,再根据三角形面积公式,即可解答
(3)过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() ,根据题意得出
,根据题意得出![]() ,根据
,根据![]() ,即可解答
,即可解答
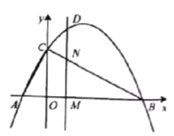
(4)当![]() 时,
时,![]() ,此时
,此时![]() 点在二次函数的对称轴上,以
点在二次函数的对称轴上,以![]() 点为圆心,
点为圆心,![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() 两点,得出
两点,得出![]() ,再根据
,再根据![]() (同弧所对圆周角),即可解答
(同弧所对圆周角),即可解答
(1)将点![]() 代入
代入![]() ,得:
,得:
![]()
解得:
所以,二次函数的表达方式为:![]()
(2)![]()
又![]()
设![]() 的解析式为:
的解析式为:![]() ,将点
,将点![]() 代入,得:
代入,得:

所以,直线![]() 的解析式为:
的解析式为:![]() .
.
将![]() 分别代入
分别代入![]() 和
和![]() 中,得:
中,得:![]() .
.
![]()
![]() .
.
(3)假设过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 的延长线于点
的延长线于点![]() ,
,
设![]() ,由题意得:
,由题意得:
![]()
![]()

所以,点![]() 的坐标为:
的坐标为:![]()
(4)当![]() 时,
时,![]() ,此时
,此时![]() 点在二次函数的对称轴上,
点在二次函数的对称轴上,
以![]() 点为圆心,
点为圆心,![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() 两点
两点
![]()
![]()
![]() 点在该圆上
点在该圆上
![]()
![]()
![]() (同弧所对圆周角)
(同弧所对圆周角)
![]()
![]()
![]() 或
或![]()

【题目】(生活观察)甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价 | ||
质量 | 金额 | |
甲 |
|
|
乙 |
|
|
菜价 | ||
质量 | 金额 | |
甲 |
| ____元 |
乙 | ____千克 |
|
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价![]() 总金额总质量)
总金额总质量)
(数学思考)设甲每次买质量为![]() 千克的菜,乙每次买金额为
千克的菜,乙每次买金额为![]() 元的菜,两次的单价分别是
元的菜,两次的单价分别是![]() 元
元![]() 千克、
千克、![]() 元
元![]() 千克,用含有
千克,用含有![]() 、
、![]() 、
、![]() 、
、![]() 的式子,分别表示出甲、乙两次买菜的均价
的式子,分别表示出甲、乙两次买菜的均价![]() 、
、![]() .比较
.比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(知识迁移)某船在相距为![]() 的甲、乙两码头间往返航行一次,在没有水流时,船的速度为
的甲、乙两码头间往返航行一次,在没有水流时,船的速度为![]() 所需时间为:如果水流速度为
所需时间为:如果水流速度为![]() 时(
时(![]() ),船顺水航行速度为(
),船顺水航行速度为(![]() ),逆水航行速度为(
),逆水航行速度为(![]() ),所需时间为
),所需时间为![]() 请借鉴上面的研究经验,比较
请借鉴上面的研究经验,比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.