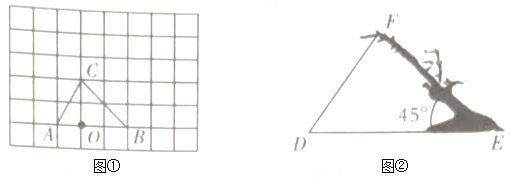题目内容
【题目】阅读下面材料：
定义：与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.
问题：⊙O的半径为1，画一个⊙O的关联图形.
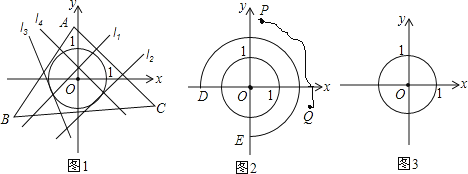
在解决这个问题时，小明以O为原点建立平面直角坐标系xOy进行探究，他发现能画出很多⊙O的关联图形，例如：⊙O本身和图1中的△ABC(它们都是封闭的图形)，以及图2中以O为圆心的
(它是非封闭的形)，它们都是⊙O的关联图形.而图2中以P，Q为端点的一条曲线就不是⊙O的关联图形.
参考小明的发现，解决问题：
(1)在下列几何图形中，①⊙O的外切正多边形；②⊙O的内接正多边形；③⊙O的一个半径大于1的同心圆；⊙O的关联图形是______(填序号).
(2)若图形G是⊙O的关联图形，并且它是封闭的，则图形G的周长的最小值是____.
(3)在图2中，当⊙O的关联图形的弧长最小时，经过D，E两点的直线为y＝____.
(4)请你在备用图中画出一个⊙O的关联图形，所画图形的长度l小于(2)中图形G的周长的最小值，并写出l的值(直接画出图形，不写作法).
【答案】（1）①③；（2）2π；（3）y=-x-
；（4）π+2.
【解析】
（1）根据与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形，可得答案;
（2）根据圆的关联图形周长，可得封闭的关联图形，根据圆的关联图形的周长最小是它本身，可得答案；
（3）根据⊙O的关联图形 
的弧长最小，可得DE是圆O的切线，可得答案;
（4）根据圆的关联图形的长度小于2π，可得圆的关联图形是非封闭的，可得答案．
解：（1）①⊙O的外切正多边形与圆的所有切线和割线都有公共点，故①说法正确；
②⊙O的内接正多边形与圆的有的切线没有公共点，故②说法错误；
③⊙O的一个半径大于1的同心圆与圆的所有切线和割线都有公共点，故③说法正确；
故答案为：①③；
（2）若图形G是⊙O的关联图形，并且它是封闭的，则图形G是它本身，图形G的周长的最小值是2π， 故答案为：2π；
（3）由当⊙O的关联图形的弧长最小时，得DE是圆的一条切线且OD=OE，
设DE的解析式是y=-x+b，由DE于圆相切，得
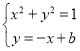
解得b=-， 故答案为：y=-x-；
（4）如图：画图形是非封闭的，l长度=π+2：
