题目内容
【题目】如图①,在![]() 的网格图中,每个小正方形的边长均为
的网格图中,每个小正方形的边长均为![]() ,点
,点![]() 和
和![]() 的顶点均为小正方形的顶点.
的顶点均为小正方形的顶点.
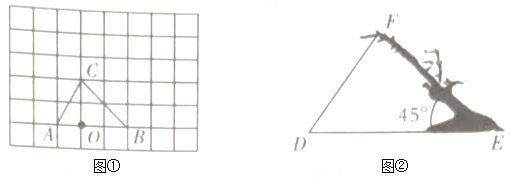
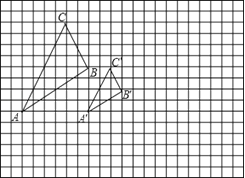
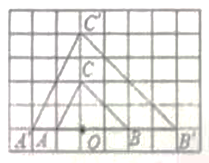
(1)以点O为位似中心,在网格图中作△ABC,使它与△ABC位似,且相似比为2;
(2)如图②,某台风过后,李明发现一棵被吹倾斜的大树![]() 与地面的夹角为
与地面的夹角为![]() ,且其影子
,且其影子![]() 长为4.5米,同时李明还发现大树树干和影子形成的△DEF与△ABC相似(树干对应
长为4.5米,同时李明还发现大树树干和影子形成的△DEF与△ABC相似(树干对应![]() 边),求大树在被吹倾斜前的高度.(结果保留根号)
边),求大树在被吹倾斜前的高度.(结果保留根号)
【答案】(1)见解析;(2)![]() 米
米
【解析】
(1)根据位似三角形的性质画图即可;
(2)先利用小正方形的边长和勾股定理求出AB、BC的长,再根据相似三角形的性质即可求出大树在被吹倾斜前的高度.
解:(1)如图所示,根据△ABC与△ABC位似,且相似比为2,分别将OA、OB、OC延长一倍,即可得到A、B、C,![]() 即为所求;
即为所求;
(2)∵![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.
故大树在被吹倾斜前的高度为![]() 米.
米.

【题目】某服装公司的某种运动服每月的销量与售价的关系信息如表:
售价x(元/件) | 100 | 110 | 120 | 130 | … |
月销量y(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:
①销量该运动服每件的利润是 元;
②月销量是y= ;(直接写出结果)
(2)设销售该运动服的月利润为w元,那么售价为多少时,当月的利润最大,最大利润时多少?
(3)该公司决定每销售一件运动服,就捐赠a(a>0)元利润给希望工程,物价部门规定该运动服售价不得超过120元,设销售该运动服的月利润为w元,若月销售最大利润是8800元,求a的值.
【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.

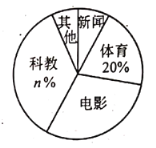
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.