题目内容
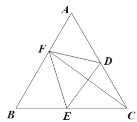
【题目】如图，已知
中，
，将斜边BC绕点B顺时针方向旋转至BD，使
,
，过点D作
，
于点E．
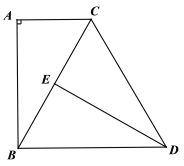
(1)求证
；
(2)若
，
，求在上述旋转过程中，线段BC扫过的面积．
【答案】（1）详见解析；(2) 6π
【解析】
（1）由旋转的性质可得BC=BD，由AD//BC可得∠ACB=∠CBD，再结合直角三角形即可完成证明；
（2）由
可得AC=BE=3，再根据30角所对的直角边等于斜边的一半得出BD=2BE=6，根据平行线的性质求出∠DBC=60°，再代入扇形面积公式求解即可求解.
（1）证明：∵
将斜边BC绕点B顺时针方向旋转至BD
∴∠A=∠BED=90°
又∵AD//BC
∴∠ACB=∠CBD
在
中
∠A=∠BED=90°，∠ACB=∠CBD，BC=BD
∴（AAS）
(2)∵
∴AC=BE=3，
∴BD=2BE=6
又∵∠DBC=90°-30°=60°
∴线段BC扫过的面积为：
=6π
练习册系列答案
相关题目
【题目】某服装公司的某种运动服每月的销量与售价的关系信息如表：
售价x（元/件） | 100 | 110 | 120 | 130 | … |
月销量y（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元，设售价为x元．
（1）请用含x的式子表示：
①销量该运动服每件的利润是 元；
②月销量是y＝ ；（直接写出结果）
（2）设销售该运动服的月利润为w元，那么售价为多少时，当月的利润最大，最大利润时多少？
（3）该公司决定每销售一件运动服，就捐赠a（a＞0）元利润给希望工程，物价部门规定该运动服售价不得超过120元，设销售该运动服的月利润为w元，若月销售最大利润是8800元，求a的值．
