题目内容
【题目】(1)在![]() 中,
中,![]() ,
,![]() 是平面内任意一点,将线段
是平面内任意一点,将线段![]() 绕点
绕点![]() 顺时针旋转与
顺时针旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,连接
,连接![]() .
.
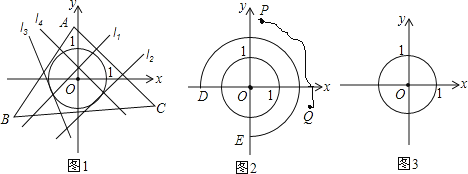
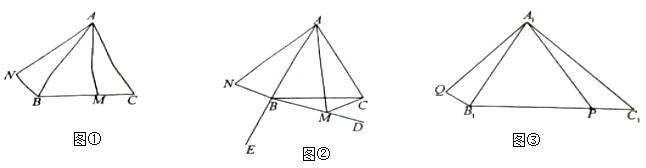
①如图①,若![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() ,
,![]() ,则
,则![]() 的大小
的大小![]() (度),
(度),![]() 的长
的长![]() ;
;
②如图②,点![]() 是
是![]() 延长线上的一点,若
延长线上的一点,若![]() 是
是![]() 内部射线
内部射线![]() 上任意一点,连接
上任意一点,连接![]() ,
,![]() 与
与![]() 的数量关系是什么?
的数量关系是什么?![]() 与
与![]() 的数量关系是什么?并分别给予证明:
的数量关系是什么?并分别给予证明:
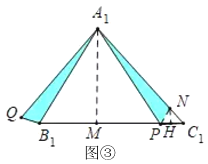
(2)如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的任意一点,连接
上的任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,求线段
,求线段![]() 长度的最小值(直接写出结果即可).
长度的最小值(直接写出结果即可).
【答案】(1)①![]() , 2;②
, 2;②![]() ,
,![]() ;证明见解析;(2)
;证明见解析;(2)![]()
【解析】
(1)①根据旋转的性质可得∠NAM=∠BAC,AN=AM,然后可得∠NAB=∠MAC=20°,再利用SAS证明![]() 即可得到NB=MC=2;
即可得到NB=MC=2;
②同①证明![]() 即可;
即可;
(2)如图③,在A1C1上截取A1N=A1B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M,利用全等三角形的判定和性质证明B1Q=PN,推出当PN的值最小时, B1Q的值最小,解直角三角形求出NH的值即可解决问题.
解:(1)①由题意可得:∠NAM=∠BAC,
∴∠NAM-∠BAM =∠BAC-∠BAM,即∠NAB=∠MAC=20°,
又∵AN=AM,AB=AC,
∴![]() ,
,
∴NB=MC=2,
故答案为:20,2;
②![]() ,
,![]() ;
;
证明:![]() 将线段
将线段![]() 绕点
绕点![]() 顺时针旋转与
顺时针旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,
,
![]() ,
,
∴∠NAM-∠BAM =∠BAC-∠BAM,
![]() ,
,
在![]() 和
和![]() 中,
中,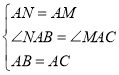 ,
,
![]() ,
,
![]() ;
;
(2)如图③,在A1C1上截取A1N=A1B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.
∵∠C1A1B1=∠PA1Q,
∴∠QA1B1=∠PA1N,
∵A1Q=A1P,A1B1=A1N,
∴△QA1B1≌△PA1N(SAS),
∴B1Q=PN,
∴当PN的值最小时, B1Q的值最小,
在Rt△A1B1M中,
∵∠A1B1M=60°,A1B1=8,
∴A1M=A1B1sin60°=![]() ,
,
∵∠MA1C1=∠B1A1C1∠B1A1M=75°30°=45°,
∴A1C1=![]() ,
,
∴NC1=A1C1A1N=![]() ,
,
在Rt△NHC1,
∵∠C1=45°,
∴NH=![]() ,
,
根据垂线段最短可知,当点P与H重合时,PN的值最小,
∴B1Q的最小值为![]() .
.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】二次函数![]() 中(
中(![]() ,
,![]() 是常数)的自变量
是常数)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| …… |
| 0 | 1 | 2 | 3 | 4 | …… |
| …… | 10 | 5 | 2 | 1 | 2 | 5 | …… |
下列结论正确的是:
A.当![]() 时,
时,![]() 有最大值1
有最大值1
B.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
C.点![]() 在该函数的图像上
在该函数的图像上
D.若![]() ,
,![]() 两点都在该函数的图象上,则当
两点都在该函数的图象上,则当![]() 时,
时,![]() .
.
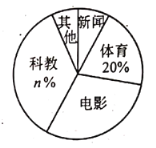
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.