题目内容
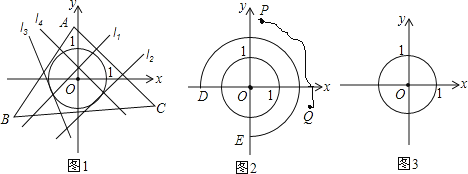
【题目】如图,⊙O的半径为2,O到顶点A的距离为5,点B在⊙O上,点P是线段AB的中点,若B在⊙O上运动一周.
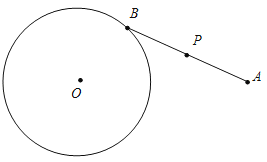
(1)点P的运动路径是一个圆;
(2)△ABC始终是一个等边三角形,直接写出PC长的取值范围.
【答案】(1)见解析;(2)![]() ≤PC≤
≤PC≤![]()
【解析】
(1)连接OA、OB,取OA的中点H,连接OB,HP,则HP是△ABO的中位线,得出HP=![]() OB=1,即P点到H点的距离固定为1,即可得出结论;
OB=1,即P点到H点的距离固定为1,即可得出结论;
(2)由等边三角形的性质和直角三角形的性质分别求出PC的最小值和最大值即可.
(1)解:连接OA、OB,取OA的中点H,连接HP,如图1所示:
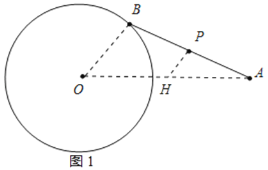
则HP是△ABO的中位线,
∴HP=![]() OB=1,
OB=1,
∴P点到H点的距离固定为1,
∴B在⊙O上运动一周,点P运动的路径是以点H为圆心,半径为1的一个圆;
(2)解:连接AO并延长AO交⊙O于点M、N,如图2所示:
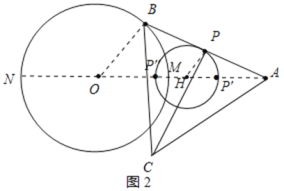
∵△ABC是等边三角形,点P是线段AB的中点,
∴PC⊥AB,PA=PB=![]() AB=
AB=![]() BC,
BC,
∴PC=![]() PA=
PA=![]() AB,
AB,
当点B运动到点M位置时,点P运动到点P'位置,PC最短,
∵AM=OA﹣OM=5﹣2=3,
∴AP'=![]() AM=
AM=![]() ,
,
∴PC=![]() ;
;
当点B运动到点N位置时,点P运动到点P'位置,PC最长,
∵AN=OA+ON=5+2=7,
∴AP'=![]() AN=
AN=![]() ,
,
∴PC=![]() ;
;
∴PC长的取值范围是![]() ≤PC≤
≤PC≤![]() .
.

【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.