题目内容

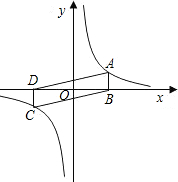
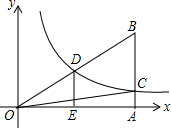
如图，已知双曲线y=
k
x
与直角三角形OAB的斜边OB相交于D，与直角边AB相交于C．若BC：CA=2：1，△OAB的面积为8，则△OED的面积为（　　）
A．
4
3
B．2C．
8
3
D．4

∵△BOC的BC边上的高为AO，△COA的AC边上的高为AO，
又∵BC：CA=2：1，
∴S△BOC：S△COA=2：1，
∴S△COA=8×
1
3
=
8
3
．
∵依据比例系数k的几何意义可得两个三角形的面积都等于
1
2
|k|，
∴S△OED=S△COA=
8
3
．
故选C．
练习册系列答案
相关题目
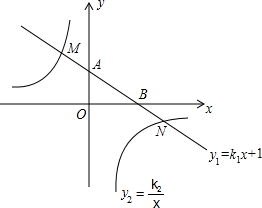如图，在平面直角坐标系xOy中，一次函数y1=k1x+1的图象与y轴交于点A，与x轴交于点B，与反比例函数y2=
k2
x
的图象分别交于点M、N，已知△AOB的面积为1，点M的纵坐标为2．
（1）求一次函数与反比例函数的解析式；
（2）直接写出y1＞y2时x的取值范围．
如图所示，设A为反比例函数y=
k
x
图象上一点，且矩形ABOC的面积为6，则这个函数的解析式为______．
如图所示，已知一次函数y=kx+b与反比例函数y=
m
x
的图象交于点A（-3，1），B（1，n）．
（1）求反比例函数及一次函数的解析式；
（2）根据图象写出一次函数的值大于反比例函数值的x的取值范围．
如图所示，已知一次函数y1=ax+b和反比例函数y2=
k
x
的图象交于A（2，1）和B（-1，-2）两点．
（1）求y1和y2的函数关系式．
（2）利用图象直接写出y1＞y2时，自变量x的取值范围．
反比例函数y=
k
x
（k＞0）的图象如图所示，A（-3，a），B（-2，b）是该图象上的两点．
（1）比较a与b的大小；
（2）若a，b两数中较大的数比较小的数大2，求这个反比例函数的解析式．
如图，A，C是函数y=
k
x
（k≠0）的图象上关于原点对称的任意两点，AB，CD垂直于x轴，垂足分别为B，D，那么四边形ABCD的面积S是（　　）
A．
k
2
B．2kC．4kD．k
如图，正比例函数y=x与反比例函数y=
4
x
的图象交于A，B两点，过点A作AC⊥x轴于点C，则△BOC的面积是（　　）
A．4B．3C．2D．1
作函数y=
5
x
(x＜0)的图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网