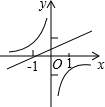题目内容
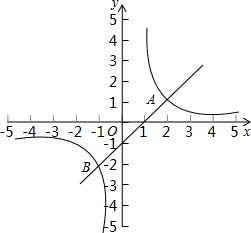
如图,在平面直角坐标系xOy中,一次函数y1=k1x+1的图象与y轴交于点A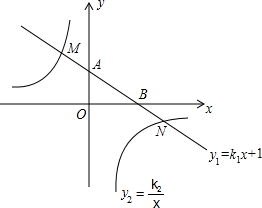 ,与x轴交于点B,与反比例函数y2=
,与x轴交于点B,与反比例函数y2=
的图象分别交于点M、N,已知△AOB的面积为1,点M的纵坐标为2.
(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时x的取值范围.
 ,与x轴交于点B,与反比例函数y2=
,与x轴交于点B,与反比例函数y2=| k2 |
| x |
(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时x的取值范围.
(1)∵一次函数y1=k1x+1的图象与y轴交于点A ,与x轴交于点B,
,与x轴交于点B,
∴A(0,1),B(-
,0).
∵△AOB的面积为1,
∴
×OB×OA=1,
×(-
)×1=1,
∴k1=-
,
∴一次函数的解析式为y1=-
x+1;
当y=2时,-
x+1=2,解得x=-2,
∴M的坐标为(-2,2).
∵点M在反比例函数的图象上,
∴k2=-2×2=-4,
∴反比例函数的解析式为y2=-
;
(2)解方程组
,
得
或
,
故当y1>y2时,x<-2或0<x<4.
 ,与x轴交于点B,
,与x轴交于点B,∴A(0,1),B(-
| 1 |
| k1 |
∵△AOB的面积为1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| k1 |
∴k1=-
| 1 |
| 2 |
∴一次函数的解析式为y1=-
| 1 |
| 2 |
当y=2时,-
| 1 |
| 2 |
∴M的坐标为(-2,2).
∵点M在反比例函数的图象上,
∴k2=-2×2=-4,
∴反比例函数的解析式为y2=-
| 4 |
| x |
(2)解方程组
|
得
|
|
故当y1>y2时,x<-2或0<x<4.

练习册系列答案
相关题目
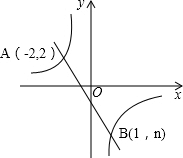
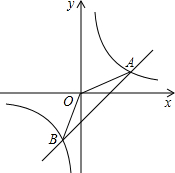 象的交点.
象的交点.