题目内容
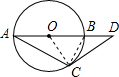
已知圆O的半径为5，AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连接AC，若∠CAB=30°，则BD的长为______．
连接OC，BC，
∵AB是圆O的直径，DC是圆O的切线，C是切点，
∴∠ACB=∠OCD=90°，
∵∠CAB=30°，
∴∠COD=2∠A=60°，CD=OC•tan∠COD=5
，
由切割线定理得，CD2=BD•AD=BD（BD+AB），
∴BD=5．
故答案为：5．
∵AB是圆O的直径，DC是圆O的切线，C是切点，
∴∠ACB=∠OCD=90°，
∵∠CAB=30°，
∴∠COD=2∠A=60°，CD=OC•tan∠COD=5
| 3 |
由切割线定理得，CD2=BD•AD=BD（BD+AB），
∴BD=5．
故答案为：5．
练习册系列答案
名校课堂系列答案
相关题目
