题目内容
已知，点C在以AB为直径的半圆上，∠CAB的平分线AD交BC于点D，⊙O经过A、D两点，且圆心O在AB上．
（1）求证：BD是⊙O的切线．
（2）若
=
，BC=4
，求⊙O的面积．
（1）求证：BD是⊙O的切线．
（2）若
| AC |
| AB |
| 1 |
| 4 |
| 5 |
（1）连接OD．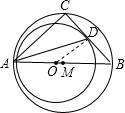
∵AB为直径，
∴∠ACB=90°，
∵OA=OD，
∴∠ODA=∠OAD，
∵AD平分∠CAB，
∴∠OAD=∠CAD，
∴∠ODA=∠CAD，
∴OD∥AC，
∴∠ODB=∠ACB=90°，
∴BD是⊙O的切线．
（2）∵
=
，
∴AB=4AC，
∵BC2=AB2-AC2，
∴15AC2=80，
∴AC=
，
∴AB=4
．
设⊙O的半径为r，
∵OD∥AC，
∴△BOD∽△BAC，
∴
=
∴
=
，解得：r=
∴πr2=π•（
）2=
π，
∴⊙O的面积为
π．
∵AB为直径，
∴∠ACB=90°，
∵OA=OD，
∴∠ODA=∠OAD，
∵AD平分∠CAB，
∴∠OAD=∠CAD，
∴∠ODA=∠CAD，
∴OD∥AC，
∴∠ODB=∠ACB=90°，
∴BD是⊙O的切线．
（2）∵
| AC |
| AB |
| 1 |
| 4 |
∴AB=4AC，
∵BC2=AB2-AC2，
∴15AC2=80，
∴AC=
|
∴AB=4
|
设⊙O的半径为r，
∵OD∥AC，
∴△BOD∽△BAC，
∴
| OB |
| AB |
| OD |
| AC |
∴
4
| ||||
4
|
| r | ||||
|
16
| ||
| 15 |
∴πr2=π•（
16
| ||
| 15 |
| 256 |
| 75 |
∴⊙O的面积为
| 256 |
| 75 |
练习册系列答案
相关题目
m，0）且垂直于x轴，当P点在x轴上移动时，直线MN也随着平行移动．按下面条件求m的值或范围．
