Question

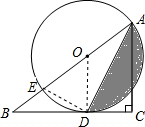
如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以AE为直径的⊙O与BC相切于点D．
（1）求证：AD平分∠BAC；
（2）若AD=2

3

，AE=4，求图中阴影部分的面积．

Answer 1

（1）证明：连接OD，则OA=OD，
∴∠DAO=∠ODA．
∵BC是⊙O的切线，
∴OD⊥BC，
∵∠C=90°，
即AC⊥BC，
∴OD∥AC，
∴∠CAD=∠ODA，
∴∠DAO=∠CAD，
∴AD平分∠BAC；

（2）连接ED，
∵AE为直径，
∴∠ADE=∠C=90°，
∵DE²=AE²-AD²=4，
∴DE=2，
在Rt△ADE中，∵AE=4，AD=2

3

，
∴DE=2，
∴∠DAE=30°，∠AOD=120°，
∴S_△AOD=

1

2

S_△ADE=

1

2

×

1

2

AD•DE=

1

2

×

1

2

×2

3

×2=

3

，
∵S_扇形AOD=

120π×22

360

=

4

3

π，
∴S_阴影=S_扇形AOD-S_△AOD=

4

3

π-

3

．