题目内容
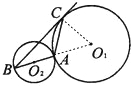
如图，已知⊙O1与⊙O2外切于A，AB是⊙O2的直径，BC切⊙O1于C，若∠B=30°，BC=6
．
求：（1）∠BCA的度数；（2）⊙O1与⊙O2的半径．
| 3 |
求：（1）∠BCA的度数；（2）⊙O1与⊙O2的半径．
（1）连接O1C，O1A，则O1C⊥BC，O2，A，O1共线，
在Rt△BCO1中，
∵∠B=30°，BC=6
，
∴∠AO1C=60°，O1B=2O1C．
∵O1A=O1C，
∴AB=AC=AO1
∴∠BCA=∠B．
∴∠BCA=30°．
（2）在Rt△BCO1中，
∵∠B=30°，BC=6
，
∴O1C=tan∠B×BC=6，O1B=2O1A=
=12．
∵O1A=O1C=6，
∴AB=O1B-O1A=6．
∴O2A=
AB=3．
∴⊙O1，⊙O2半径分别为6和3．
在Rt△BCO1中，
∵∠B=30°，BC=6
| 3 |
∴∠AO1C=60°，O1B=2O1C．
∵O1A=O1C，
∴AB=AC=AO1
∴∠BCA=∠B．
∴∠BCA=30°．
（2）在Rt△BCO1中，
∵∠B=30°，BC=6
| 3 |
∴O1C=tan∠B×BC=6，O1B=2O1A=
| BC |
| cos∠B |
∵O1A=O1C=6，
∴AB=O1B-O1A=6．
∴O2A=
| 1 |
| 2 |
∴⊙O1，⊙O2半径分别为6和3．
练习册系列答案
阅读快车系列答案
相关题目
m，0）且垂直于x轴，当P点在x轴上移动时，直线MN也随着平行移动．按下面条件求m的值或范围．
，交AY于点D．