题目内容
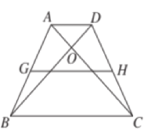
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD于点O,梯形的高为10cm,求梯形中位线的长.
【答案】10cm.
【解析】
首先根据ABCD是等腰梯形且AC⊥BD,得出△DBE是等腰直角三角形,再根据等腰直角三角形三线合一的性质,得出BE=20,从而得出AD+BC=20,再根据梯形中位线的性质即可解答.
过点D作DE∥AC,交BC的延长线于点E,则四边形ACED是平行四边形,作DF⊥BE于点F,则DF=10.
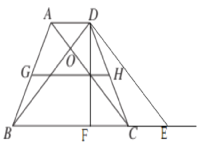
∵四边形ACED是平行四边形,
∴AD=CE.
∵ABCD是等腰梯形,
∴BD=AC=DE.
∵AC⊥BD,
∴DE⊥BD,
∴△DBE是等腰直角三角形.
∵DF=10,
∴BE=20,
即AD+BC=20,
∴梯形的中位线为10cm.

练习册系列答案
相关题目