题目内容
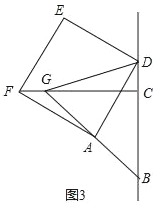
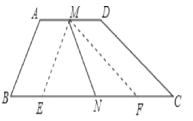
【题目】如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°，点M、N分别是AD、BC的中点，如果BC=10，AD=4，那么MN的长是___.
【答案】3
【解析】
由于∠C与∠B的和为90°，故此可以过M点分别作AB、DC的平行线交BC于点E、F，构造出一个直角三角形，所求的线段MN是Rt△MEF的中线，只需求出斜边EF的长度即可，根据EF=BC-(BE+FC)=BC-AD，计算出EF即可.
过点M分别作AB、CD的平行线交BC于点E、F，
∵EM∥AB，FM∥DC，
∴∠MEF=∠B=54°，∠MFE=∠C=36°，
∴∠EMF=180°-54°-36°=90°.
∵AD∥BC，
∴四边形AMEB、四边形MFCD均为平行四边形，
∴BE=AM，CF=MD，
∴BE+CF=AD=4.
∵BC=10，
∴EF=6.
在Rt△MEF中，N为EF中点，
∴MN=
EF=3.
故答案为：3.
练习册系列答案
相关题目
【题目】为了解宣城市市民“绿色出行”方式的情况，我校数学兴趣小组以问卷调查的形式，随机调查了宣城市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
种类 |
|
|
|
|
|
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
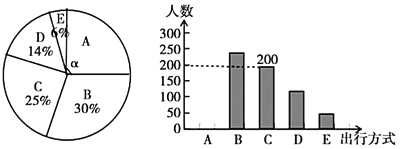
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有______人，其中选择
类的人数有______人；
（2）在扇形统计图中，求
类对应扇形圆心角
的度数，并补全条形统计图；
（3）宣城市约有人口280万人，若将、、
这三类出行方式均视为“绿色出行”方式，请估计我市“绿色出行”方式的人数．
