题目内容
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.

(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.请画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).
【答案】(1)通过三角形全等进而求证(2)DE-BF=AF-AE=EF
【解析】
试题考查知识点:正方形;三角形的全等与相似;等量代换
思路通过利用正方形的性质,证明三角形的全等与相似,然后利用等量代换。
具体解答过程:
(1)、∵四边形ABCD是正方形
∴∠BAD=90°,AB=AD
∵DE⊥AG,BF⊥AG
∴∠AFB=∠DEA=90°
∵∠AFB+∠DAE=90°,∠ADE+∠DAE=90°
∴∠AFB=∠ADE
∴Rt△AFB≌Rt△DEA
∴DE=AF,AE=BF
∴DE-BF=AF-AE=EF
(2)、当点G为BC边中点时,如下图所示。
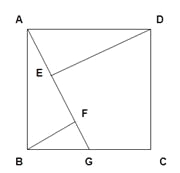
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,AB:BG=2:1
∵∠AFB=∠ADE
∴Rt△AFB≌Rt△DEA∽Rt△ABG∽Rt△BFG
∴AE=BF,AF=DE=2AE,BF=2FG,AE=EF
∴EF=2FG
(3)、如下图所示。
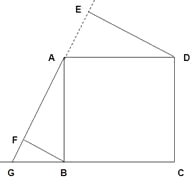
∵DE⊥AG,BF⊥AG
∴∠AFB=∠DEA=90°
∵∠BAD=90°,∠EAF是平角,
∴∠EAD+∠FAB=90°
∵∠EAD+∠EDA=90°
∴∠FAB=∠EDA
∴Rt△AFB≌Rt△DEA
∴AE=BF,DE=AF
∴EF=EA+AF即EF=DE+BF

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】经过实验获得两个变量 x(x 0), y( y 0) 的一组对应值如下表。
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 7 | 3.5 | 2.33 | 1.75 | 1.4 | 1.17 | 1 |
(1)在网格中建立平面直角坐标系,画出相应的函数图象,求出这个函数表达式;
(2)结合函数图象解决问题:(结果保留一位小数)

①![]() 的值约为多少?
的值约为多少?
②点A坐标为(6,0),点B在函数图象上,OA=OB,则点B的横坐标约是多少?