Question

【题目】如图，有一圆柱，其高为12cm，它的底面半径为3cm，在圆柱下底面A处有一只蚂蚁，它想得到上面B处的食物，则蚂蚁经过的最短距离为_________.（π取3）

Answer 1

【答案】15cm．

【解析】本题应先把圆柱展开即得其平面展开图，则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πr，蚂蚁经过的最短距离为连接A，B的线段长，由勾股定理求得AB的长．

解：如图所示，

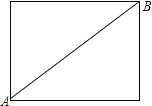
圆柱展开图为长方形，
则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πrcm，
蚂蚁经过的最短距离为连接A，B的线段长，
由勾股定理得AB===15cm．
故蚂蚁经过的最短距离为15cm．（π取3）

“点睛”解答本题的关键是计算出圆柱展开后所得长方形长和宽的值，然后用勾股定理计算即可．